Bài 1 trang 137 SGK Vật lí 12

Cho \((u_n)\) là một cấp số cộng có sáu số hạng với \(\displaystyle u_1 ={{ - 1} \over 3},d = 3\). Viết dạng khai triển của nó.

Biết bốn số hạng đầu của một dãy số là -1, 3, 7, 11.

Từ đó hãy chỉ ra một quy luật rồi viết tiếp năm số hạng của dãy theo quy luật đó.

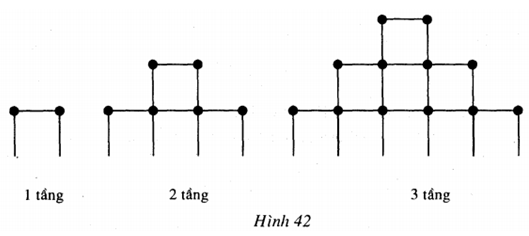
Mai và Hùng chơi trò xếp các que diêm thành hình tháp trên mặt sân. Cách xếp được thể hiện trên Hình 42.

Hỏi: Nếu tháp có 100 tầng thì cần bao nhiêu que diêm để xếp tầng đế của tháp?

Cấp số cộng gồm tám số hạng -1, 3, 7, 11, 15, 19, 23, 27 được viết vào bảng sau:

b) Tính tổng các số hạng của cấp số cộng.a) Hãy chép lại bảng trên và viết các số hàn của cấp số đó vào dòng thứ hai theo thứ tự ngược lại. Nêu nhận xét về tổng của các số hạng ở mỗi cột.

Trong các dãy số sau đây, dãy số nào là cấp số cộng? Tính số hạng đầu và công sai của nó:

a) \(u_n= 5 - 2n\);            b) \(u_n=  \dfrac{n}{2}- 1\);

c) \(u_n= 3^n\);                    d) \(u_n=  \dfrac{7-3n}{2}\)

Tìm số hạng đầu và công sai của các cấp số cộng sau, biết:

\(a)\,\,\left\{ \begin{array}{l}{u_1} - {u_3} + {u_5} = 10\\{u_1} + {u_6} = 17\end{array} \right.\\b)\,\,\left\{ \begin{array}{l}{u_7} - {u_3} = 8\\{u_2}.{u_7} = 75\end{array} \right.\)

Trong các bài toán về cấp số cộng, ta thường gặp năm đại lượng \(u_1, n, d, u_n, S_n\).

a) Hãy viết các hệ thức liên hệ giữa các đại lượng để có thể tìm được các đại lượng còn lại?

b) Lập bảng theo mẫu sau và điền vào chỗ trống thích hợp:

Mặt sàn tầng một của một ngôi nhà cao hơn mặt sân \(0,5 m\). Cầu thang đi từ tầng một lên tầng \(2\) gồm \(21\) bậc, mỗi bậc cao \(18 cm\).

a) Hãy viết công thức để tìm độ cao của một bậc tuỳ ý so với mặt sân.

b) Tính độ cao của sàn tầng hai so với mặt sân.

Từ \(0\) giờ đến \(12\) giờ trưa, đồng hồ đánh bao nhiêu tiếng, nếu nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ.