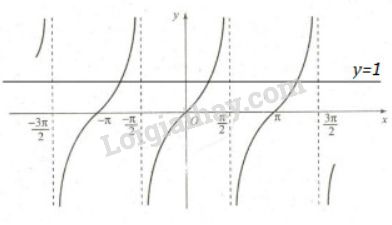
Trong đoạn \(\displaystyle\left[ { - \pi ;{{3\pi } \over 2}} \right]\),
a) Trục hoành cắt đồ thị hàm số \(y = \tan x\) tại ba điểm có hoành độ \(- π ; 0 ; π\).
Vậy \(x = - π; x = 0 ; x = π\).
b) Đường thẳng \(y = 1\) cắt đồ thị \(y = \tan x\) tại ba điểm có hoành độ \(\displaystyle {\pi \over 4};{\pi \over 4} \pm \pi \).
Vậy \(\displaystyle x = - {{3\pi } \over 4};\,\,x = {\pi \over 4};\,\,x = {{5\pi } \over 4}\).
c) Trong các khoảng \(\displaystyle\left( { - \pi ; - {\pi \over 2}} \right)\); \(\displaystyle\left( {0;{\pi \over 2}} \right)\); \(\displaystyle \left( {\pi ;{{3\pi } \over 2}} \right)\), đồ thị hàm số nằm phía trên trục hoành.
Vậy \(\displaystyle x \in \left( { - \pi ; - {\pi \over 2}} \right) \cup \left( {0;{\pi \over 2}} \right) \cup \left( {\pi ;{{3\pi } \over 2}} \right)\).
d) Trong các khoảng \(\displaystyle\left( { - {\pi \over 2};0} \right),\left( {{\pi \over 2};\pi } \right)\), đồ thị hàm số nằm phía dưới trục hoành.
Vậy \(\displaystyle x \in \left( { - {\pi \over 2};0} \right) \cup \left( {{\pi \over 2};\pi } \right)\).