Bài 19.4, 19.5, 19.6 trang 46 SBT Vật lí 10

Câu 19.4.

Một người đang quẩy trên vai một chiếc bị có trọng lượng 50 N. Chiếc bị buộc ở đầu gậy cách vai 60 cm. Tay người giữ ở đầu kia cách vai 30 cm. Bỏ qua trọng lượng của gậy (H.19.2).

a) Hãy tính lực giữ của tay.

b) Nếu dịch chuyển gậy cho bị cách vai 30 cm và tay cách vai 60 cm, thì lực giữ bằng bao nhiêu ?

c) Trong hai trường hợp trên, vai người chịu một áp lực bằng bao nhiêu ?

a.  \(\displaystyle{F \over P} = {{60} \over {30}} = 2 = > F = 2P = 100(N)\)

b. \(\displaystyle{F \over P} = {{30} \over {60}} = {1 \over 2} = > F = {1 \over 2}P = 25(N)\)

c. Áp lực bằng \(F + P = 150 N\) hoặc \(75 N\)

Câu 19.5.

Xác định các áp lực của trục lên hai ổ trục A và B (H.19.3). Cho biết trục có khối lượng 10 kg, bánh đà đặt tại C có khối lượng 20 kg, khoảng cách AC = 1 m ; BC = 0,4 m lấy g = 10 m/s²

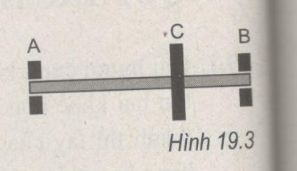
Ta phân tích trọng lực \(\overrightarrow {{P_1}} \) của trục thành hai lực thành phần tác dụng lên hai ổ trục A và B:

P_1A = P_1B = 0,5P = 50 N.

Làm tương tự với trọng lực \(\overrightarrow {{P_2}} \)  của bánh đà:

P_2A + P_2B = P₂  = 200 N(1)

\(\displaystyle{{{P_{2A}}} \over {{P_{2B}}}} = {{0,4} \over 1} = 0,4\)  (2)

Từ (1) và (2) ta được P_2A = 57 N và P_2B = 143 N.

Vậy áp lực lên ổ trục A là P_1A + P_2A = 107 N

Áp lực lên ổ trục B là P_1B + P_2B = 193 N

Câu 19.6.

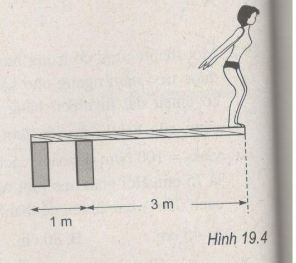
Một vận động viên nhảy cầu có khối lượng m = 60 kg đang đứng ở mép ván cầu (H.19.4). Lấy g = 10 m/s².

a) Tính momen của trọng lực của người đối với cọc đỡ trước.

b)  Tính các lực F₁ và F₂ mà hai cọc đỡ tác dụng lên ván.

Bỏ qua khối lượng của tấm ván.

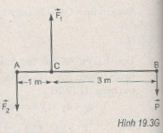
a. M = Pl = 600.3,0 = 1800 N.m

b. Momen của lực  \(\overrightarrow {{F_2}} \) của cọc đỡ sau đối với cọc đỡ trước phải cân bằng với momen của trọng lực của người. Do đó, lực \(\overrightarrow {{F_2}} \) phải hướng xuống (H.19.3G)

M_F2 = F₂d₂ = 1800 N.m

=> F₂ = 1800 N.

Hợp lực của \(\overrightarrow {{F_2}} \) và \(\overrightarrow {{P}} \) cân bằng với lực \(\overrightarrow {{F_1}} \)

F₁ = F₂ + P = 2400 N.