Bài 2 trang 142 SGK Vật lí 12

Câu 1: Chọn mệnh đề đúng trong các mệnh đề sau:

A. Nếu  \(\lim \left| {{u_n}} \right| =  + \infty \) thì \(\lim {u_n} =  + \infty \)

C. Nếu  \(\lim \left| {{u_n}} \right| =  + \infty \) thì \(\lim {u_n} =  - \infty \)

B. Nếu  \(\lim {u_n} = 0\) thì \(\lim \left| {{u_n}} \right| = 0\)

D. Nếu  \(\lim {u_n} =  - a\) thì \(\lim \left| {{u_n}} \right| = a\)

Câu 2: Giá trị của \(\lim \dfrac{{{{3.2}^n} - {3^n}}}{{{2^{n + 1}} + {3^{n + 1}}}}\)bằng

A. \( + \infty \)             B. \( - \infty \)

C. \( - \dfrac{1}{3}\)             D. 1

Câu 3: Giá trị của \(\lim \dfrac{{\sqrt {{n^2} + 1} }}{{n + 1}}\) bằng

A. \( + \infty \)               B. \( - \infty \)

C. \(0\)                    D. 1                

Câu 4: Tìm giá trị đúng của \(S = \sqrt 2 \left( {1 + \dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{8} + ... + \dfrac{1}{{{2^n}}} + ...} \right)\)

A. \(\sqrt 2  + 1\)               B. 2

C. \(2\sqrt 2 \)                   D. \(\dfrac{1}{2}\)

Câu 5: Kết quả đúng của  \(\lim \left( {5 - \dfrac{{n\cos 2n}}{{{n^2} + 1}}} \right)\)là:

A.5                     B. 4

C. -4                   D. \(\dfrac{1}{4}\)

Câu 6: Tính giới hạn: \(\lim \dfrac{{1 + 3 + 5 + ... + (2n + 1)}}{{3{n^2} + 4}}\)

A.0                    B. \(\dfrac{1}{3}\)

C. \(\dfrac{2}{3}\)                 D. 1

Câu 7: Giá trị của \(\lim \dfrac{{\cos n + \sin n}}{{{n^2} + 1}}\) bằng

A.0                    B. \( - \infty \)

C.\( + \infty \)              D. 1        

Câu 8: Cho dãy số có giới hạn \(({u_n})\)xác định bởi \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = \dfrac{1}{2}}\\{{u_{n + 1}} = \dfrac{1}{{2 - {u_n}}};n \ge 1}\end{array}} \right.\). Tìm kết quả đúng của \(\lim {u_n}\).

A.0                  B. 1

C. -1                D. \(\dfrac{1}{2}\)

Câu 9: Giá trị của \(\lim \sqrt[n]{a};\,\,\,a > 0\) bằng

A. \( + \infty \)                B. \( - \infty \)

C. \(0\)                     D. 1

Câu 10: Tính giới hạn \(\lim \left[ {\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + ... + \dfrac{1}{{n(n + 1)}}} \right]\)

A.0               B. 1

C. \(\dfrac{3}{2}\)            D. Không có giới hạn

Câu 1: Giá trị của \(\lim \dfrac{1}{{{n^k}}}\,(k \in {\mathbb{N}^*})\)bằng

A.0                 B. 2

C. 4               D. 5

Câu 2: Giá trị đúng của \(\lim ({3^n} - {5^n})\) là:

A. \( + \infty \)           B. \( - \infty \)

C. 2                 D. -2

Câu 3: Giá trị của \(\lim \dfrac{{{{\sin }^2}n}}{{n + 2}}\)bằng

A.0                 B. 3

C. 5                D. 8

Câu 4: Tính giới hạn của dãy số  \({u_n} = q + 2{q^2} + ... + n{q^n};\,\,\left| q \right| < 1\)

A. \( + \infty \)                    B. \( - \infty \)

C. \(\dfrac{q}{{{{(1 - q)}^2}}}\)            D. \(\dfrac{q}{{{{(1 + q)}^2}}}\)

Câu 5: Giá trị của \(\lim (2n + 1)\)bằng

A. \( + \infty \)                  B. \( - \infty \)

C. 0                       D. 1

Câu 6: Tính \(\lim (\sqrt {4{n^2} + n + 1}  - 2n)\)

A. \( + \infty \)                  B. \( - \infty \)

C. 3                      D. \(\dfrac{1}{4}\)

Câu 7: Giá trị của \(A = \lim \dfrac{{n - 2\sqrt n }}{{2n}}\) bằng

A. \( + \infty \)                   B. \( - \infty \)

C. \(\dfrac{1}{2}\)                      D. 1

Câu 8: Giá trị của \(A = \lim \dfrac{{{{(2{n^2} + 1)}^4}{{(n + 2)}^9}}}{{{n^{17}} + 1}}\) bằng

A. \( + \infty \)               B. \( - \infty \)

C. 16                  D. 1                  

Câu 9: Tính giới hạn của dãy số \({u_n} = \dfrac{{(n + 1)\sqrt {{1^3} + {2^3} + ... + {n^3}} }}{{3{n^3} + n + 2}}\)

A. \( + \infty \)                 B. \( - \infty \)

C. \(\dfrac{1}{9}\)                    D. 1

Câu 10: Tính giới hạn: \(\lim \left[ {\dfrac{1}{{1.3}} + \dfrac{1}{{2.4}} + ... + \dfrac{1}{{n(n + 2)}}} \right]\)

A.1                     B.0

C. \(\dfrac{2}{3}\)                  D. \(\dfrac{3}{4}\)

Câu 1: Cho hai dãy số  thỏa mãn   với mọi  và  thì:

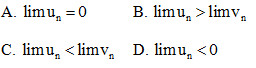
Câu 2: Trong các giới hạn sau, giới hạn nào bằng -1?

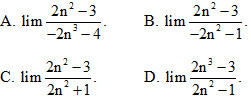
Câu 3: Chọn kết quả đúng: \(\lim \dfrac{{\dfrac{{ - 1}}{3}\sqrt n  + 2n}}{{3n}}\) bằng

A. \(\dfrac{{ - 1}}{9}\)             B. \(\dfrac{2}{3}\)

C. \( - \infty \)             D. Kết quả khác

Câu 4: Cấp số nhân lùi vô hạn\(({u_n})\) có \({u_1} =  - 1;q = x;\left| x \right| < 1\). Tìm tổng S và ba số hạng đầu của cấp số này

A. \(S = \dfrac{{ - 1}}{{1 + x}}\)và \( - 1;x; - {x^2}\)                     

B. \(S = \dfrac{{ - 1}}{{1 + x}}\)và \(1;x;{x^2}\)

C. \(S = \dfrac{{ - 1}}{{1 - x}}\)và \( - 1; - x; - {x^2}\)

D. \(S = \dfrac{{ - 1}}{{1 - x}}\)và \( - 1;x; - {x^2}\)

Câu 5: Tính \(\lim (\sqrt n  - \sqrt {n + 1} )\)

A.Không có giới hạn khi \(n \to  + \infty \)

B. 0

C. -1

D. Kết quả khác

Câu 6: Chọn kết quả đúng:

A. \(\lim \sqrt {\dfrac{{2n - 7}}{n}}  =  + \infty \)

B. \(\lim \sqrt {\dfrac{2}{n}}  = \sqrt 2 \)

C. \(\lim \sqrt {\dfrac{{2{n^2}}}{{n + 1}}}  = \sqrt 2 \)                  

D. \(\lim \sqrt {\dfrac{{n - 7}}{{2n}}}  = \dfrac{{\sqrt 2 }}{2}\)

Câu 7: Tìm \(\lim \sqrt {\dfrac{{7 - 2n}}{{4n + 5}}} \)

A. \(\sqrt {\dfrac{1}{2}} \)

B. \( - \infty \)

C. 0

D. Không có giới hạn khi \(n \to  + \infty \)

Câu 8: Giá trị của \(\lim \dfrac{{\sqrt {{n^2} + 1}  - \sqrt[3]{{3{n^3} + 2}}}}{{\sqrt[4]{{2{n^4} + n + 2}} - n}}\) bằng

A. \( + \infty \)

B. \( - \infty \)

C. \(\dfrac{{1 - \sqrt[3]{3}}}{{\sqrt[4]{2} - 1}}\)

D. 1

Câu 9: Giới hạn bằng?

A. 0                B. \(\frac{{ - 1}}{2}\)

C. \(\frac{{ - 1}}{{\sqrt 2 }}\)            D.  \(\frac{1}{{\sqrt 2 }}\)

Câu 10: Kết quả nào sau đây là đúng?

A. Cấp số nhân lùi vô hạn \(({u_n})\)có công bội q thì tổng \(S = \dfrac{u}{{1 - q}}\)

B. Cấp số nhân lùi vô hạn \(({u_n})\)có \({u_1} = 4;q = \dfrac{4}{3}\) thì tổng \(S =  - 12\)

C. Cấp số nhân lùi vô hạn \(({u_n})\)có \({u_1} = 15;S = 60\) thì \(q = \dfrac{3}{4}\)

D. Cấp số nhân lùi vô hạn \(({u_n})\)có \({u_1} =  - 4;q =  - \dfrac{5}{4}\) thì tổng \(S =  - 169\)

Câu 1: Tính \(\mathop {\lim }\limits_{x \to  - 1} \dfrac{{{x^3} + 2{x^2} + 1}}{{2{x^5} + 1}}\)

A.-2                B. \(\dfrac{{ - 1}}{2}\)

C. \(\dfrac{1}{2}\)               \(D. 2\)                                                                  

Câu 2: Tính giới hạn sau: \(\mathop {\lim }\limits_{x \to  - 1} \dfrac{{{x^2} + 2x + 1}}{{2{x^3} + 2}}\)

A. \( - \infty \)               B. 0

C. \(\dfrac{1}{2}\)                 D. \( + \infty \)

Câu 3: Tìm \(\mathop {\lim }\limits_{x \to 1} \dfrac{{\sqrt {x + 3}  - 2}}{{x - 1}}\)

A. \( + \infty \)              B. \( - \infty \)

C. -2                 D. \(\dfrac{1}{4}\)

Câu 4: Tính \(\mathop {\lim }\limits_{x \to  + \infty } \dfrac{{x + 3}}{{x - 2}}\)

A. \( + \infty \)                 B. \( - \infty \)

C. 1                      D. -2

Câu 5: Tìm a để hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{{x^2} + ax + 1}\\{2{x^2} - x + 1\,}\end{array}} \right.\,\,\,\begin{array}{*{20}{c}}{khi}\\{khi}\end{array}\,\,\,\begin{array}{*{20}{c}}{\,\,x > 2}\\{x \le 2}\end{array}\) có giới hạn khi \(x \to 2\)

A. \(\dfrac{1}{2}\)                       B. \( + \infty \)

C. \( - \infty \)                    \(D. 1\)                                           

Câu 6: Cho hàm số \(f(x) = \sqrt {\dfrac{{4{x^2} - 3x}}{{(2x - 1)({x^3} - 2)}}} \). Chọn kết quả đúng của \(\mathop {\lim }\limits_{x \to 2} f(x)\)

A. \(\dfrac{5}{9}\)                     B. \(\dfrac{{\sqrt 5 }}{3}\)

C. \(\dfrac{{\sqrt 5 }}{9}\)                  D. \(\dfrac{{\sqrt 2 }}{9}\)

Câu 7: Tính \(\mathop {\lim }\limits_{x \to {2^ - }} \dfrac{{3x - 1}}{{x - 2}}\)

A. \( + \infty \)                          B. -2

C. 1                                D. \( - \infty \)

Câu 8: Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{{x^2} - 3}\\{x - 1\,}\end{array}} \right.\,\,\,\begin{array}{*{20}{c}}{khi}\\{khi}\end{array}\,\,\,\begin{array}{*{20}{c}}{\,\,x \ge 2}\\{x < 2}\end{array}\). Chọn kết quả đúng của \(\mathop {\lim }\limits_{x \to 2} f(x)\)

A.-1                           B. 0

C. 1                           D. Không tồn tại

 Câu 9: Tính \(\mathop {\lim }\limits_{x \to  - \infty } \dfrac{{2{x^2} - x + 1}}{{x + 2}}\)

 A. \( + \infty \)                 B. \( - \infty \)

C. 1                       D. -2

Câu 10: Tìm a để hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{5a{x^2} + 3x + 2a + 1}\\{1 + x + \sqrt {{x^2} + x + 2} \,}\end{array}} \right.\,\,\,\begin{array}{*{20}{c}}{khi}\\{khi}\end{array}\,\,\,\begin{array}{*{20}{c}}{\,\,x \ge 0}\\{x < 0}\end{array}\) có giới hạn khi\(x \to 0\)

A. \( + \infty \)                   B. \( - \infty \)

C. \(\dfrac{{\sqrt 2 }}{2}\)                   D. 1

Câu 1: Tính \(\mathop {\lim }\limits_{x \to  + \infty } \dfrac{5}{{3x + 2}}\)

A.0                   B. 1

C. \(\dfrac{5}{3}\)                D. \( + \infty \)

Câu 2: Tìm giới hạn sau: \(\mathop {\lim }\limits_{x \to 1} \dfrac{{{x^3} - 3{x^2} + 2}}{{{x^2} - 4x + 3}}\)

A. \( + \infty \)                    B. \( - \infty \)

C. \(\dfrac{3}{2}\)                       D. 1

Câu 3: Cho hàm số \(f(x) = \dfrac{{x - 3}}{{\sqrt {{x^2} - 9} }}\). Giá trị đúng của \(\mathop {\lim }\limits_{x \to {3^ + }} f(x)\) là

A.0                       B. \( - \infty \)

C. \( + \infty \)                D. \(\sqrt 6 \)

Câu 4: Tính giới hạn sau: \(\mathop {\lim }\limits_{x \to  - \infty } \dfrac{{\sqrt[3]{{1 + {x^4} + {x^6}}}}}{{\sqrt {1 + {x^3} + {x^4}} }}\)

A. \( + \infty \)                   B. \( - \infty \)

C. \(\dfrac{4}{3}\)                      D. 1

Câu 5: Tính \(\mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{\sqrt {{x^2} - x + 3} }}{{2\left| x \right| - 1}}\)

A.3                         B. \(\dfrac{1}{2}\)

C. 1                        D. \( + \infty \)

Câu 6: Tìm giới hạn \(\mathop {\lim }\limits_{x \to  - \infty } x(\sqrt {4{x^2} + 1}  - x)\)

A. \( + \infty \)                   B. \( - \infty \)

C. \(\dfrac{4}{3}\)                      D. 0                   

Câu 7: Tính \(\mathop {\lim }\limits_{x \to 0} \dfrac{{{{(1 + 3x)}^3} - {{(1 - 4x)}^4}}}{x}\)

A. \(\dfrac{{ - 1}}{6}\)                   B. \( - \infty \)

C. \( + \infty \)                   D. 25

Câu 8: Tính \(\mathop {\lim }\limits_{x \to 0} \dfrac{{(1 + x)(1 + 2x)(1 + 3x) - 1}}{x}\)

A. \( + \infty \)                        B. \( - \infty \)

C. \(\dfrac{{ - 1}}{6}\)                        D. 6

Câu 9: Tính \(\mathop {\lim }\limits_{x \to 3} \dfrac{{\sqrt {2x + 3}  - x}}{{{x^2} - 4x + 3}}\)

A.1                       B. \(\dfrac{{ - 1}}{3}\)

C. \( + \infty \)                 D. \( - \infty \)

Câu 10: Tính \(\mathop {\lim }\limits_{x \to  + \infty } \dfrac{{2x - \sqrt {3{x^2} + 2} }}{{5x + \sqrt {{x^2} + 1} }}\)

A. \( + \infty \)                  B. \( - \infty \)

C. \(\dfrac{{2 - \sqrt 3 }}{6}\)           D. 0

Câu 1: Giá trị đúng của \(\mathop {\lim }\limits_{x \to 3} \dfrac{{\left| {x - 3} \right|}}{{x - 3}}\)

A.Không tồn tại      B. 0

C. 1                        D. \( + \infty \)

Câu 2: Tìm giới hạn \(D = \mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt[3]{{x + 1}} - 1}}{{\sqrt {2x + 1}  - 1}}:\)

A. \( + \infty \)                   B. \( - \infty \)

C. \(\dfrac{1}{3}\)                      D. 0

Câu 3: Tìm giới hạn  \(A = \mathop {\lim }\limits_{x \to 2} \dfrac{{2{x^2} - 5x + 2}}{{{x^3} - 3x - 2}}:\)

A. \( + \infty \)                       B. \( - \infty \)

C. \(\dfrac{1}{3}\)                           D. 1

Câu 4: \(\mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{{x^2} - x + 1}}{{{x^2} - 1}}\) bằng:

A. \( - \infty \)                      B. -1

C. 1                           D. \( + \infty \)

Câu 5: Tìm giới hạn \(E = \mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {{x^2} - x + 1}  - x} \right)\):

A. \( + \infty \)                    B. \( - \infty \)

C. \( - \dfrac{1}{2}\)                    D. 0

Câu 6: Tìm giới hạn \(E = \mathop {\lim }\limits_{x \to  - \infty } x\left( {\sqrt {4{x^2} + 1}  - x} \right)\):

A. \( + \infty \)                    B. \( - \infty \)

C. \(\dfrac{4}{3}\)                        D. 0

Câu 7: Chọn kết quả đúng của \(\mathop {\lim }\limits_{x \to {0^ - }} \left( {\dfrac{1}{{{x^2}}} - \dfrac{2}{{{x^3}}}} \right):\)

A. \( - \infty \)                    B. 0

C. \( + \infty \)                    D. Không tồn tại

Câu 8: Tìm giới hạn \(B = \mathop {\lim }\limits_{x \to  - \infty } \left( {x - \sqrt {{x^2} + x + 1} } \right)\):

 A. \( + \infty \)                    B. \( - \infty \)

C. \(\dfrac{4}{3}\)                         D. 0

Câu 9: Tìm giới hạn \(A = \mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {4x + 1}  - \sqrt[3]{{2x + 1}}}}{x}\):

A. \( + \infty \)                     B. \( - \infty \)

C. \(2\)                         D. 0

Câu 10: Tìm giới hạn \(C = \mathop {\lim }\limits_{x \to 3} \dfrac{{\sqrt[{}]{{2x + 3}} - 3}}{{{x^2} - 4x + 3}}:\)

A. \( + \infty \)                     B. \( - \infty \)

C. \(\dfrac{1}{6}\)                        D. 0

Câu 1: Tìm giới hạn  \(B = \mathop {\lim }\limits_{x \to 1} \dfrac{{{x^4} - 3x + 2}}{{{x^3} + 2x - 3}}:\)

A. \( + \infty \)                   B. \( - \infty \)

C. \(\dfrac{1}{5}\)                       D. 1

Câu 2: Cho hàm số \(f(x) = \dfrac{{{x^2} + 1}}{{{x^2} + 5x + 6}}\). Khi đó hàm số \(f(x)\)liên tục trên các khoảng nào sau đây?

A.(-3;2)                   B. \(( - 2; + \infty )\)

C. \(( - \infty ;3)\)            D.(2;3)

Câu 3: Tìm giới hạn  \(A = \mathop {\lim }\limits_{x \to 2} \dfrac{{2{x^2} - 5x + 2}}{{{x^3} - 8}}:\)

A. \( + \infty \)                      B. \( - \infty \)

C. \(\dfrac{1}{4}\)                         D. 0

Câu 4: Cho hàm số \(f(x) = \sqrt {\dfrac{{{x^2} + 1}}{{2{x^4} + {x^2} - 3}}} \). Chọn kết quả đúng của \(\mathop {\lim }\limits_{x \to  + \infty } f(x)\):

A. \(\dfrac{1}{2}\)                     B. \(\dfrac{{\sqrt 2 }}{2}\)

C. 0                       D. \( + \infty \)

Câu 5: \(\mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{\sqrt {{x^2} - x + 3} }}{{2\left| x \right| - 1}}\) bằng:

A.3                         B. \(\dfrac{1}{2}\)

C. 1                        D. \( + \infty \)

Câu 6: Tìm giới hạn \(A = \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{{{(2x + 1)}^3}{{(x + 2)}^4}}}{{{{(3 - 2x)}^7}}}\):

A. \( + \infty \)                  B. \( - \infty \)

C. \( - \dfrac{1}{{16}}\)                D. 0

Câu 7: Tính \(\mathop {\lim }\limits_{x \to  - \infty } \dfrac{{\sqrt {4{x^2} - 3x + 4}  - 2x}}{{\sqrt {{x^2} + x + 1}  - x}}\)

A.\(\dfrac{-3}{2}\)                       B. 0

C. \( + \infty \)                  D. \( - \infty \)

Câu 8: Tính \(\mathop {\lim }\limits_{x \to 0} {x^2}\cos \dfrac{2}{{nx}}\)

A.Không tồn tại         B. 0

C. 1                            D. \( + \infty \)

Câu 9: Cho hàm số \(f(x) = \dfrac{{{x^2} - 1}}{{x + 1}}\) và \(f(2) = {m^2} - 2\)với \(x \ne 2\). Giá trị của m để \(f(x)\)liên tục tại x = 2 là:

A. \(\sqrt 3 \)                     B. \( - \sqrt 3 \)

C. \( \pm \sqrt 3 \)                   D. \( \pm 3\)

Câu 10: Cho hàm số \(f(x) = \sqrt {{x^2} - 4} \). Chọn câu đúng trong các câu sau:

(1) \(f(x)\)liên tục tại x = 2

(2) \(f(x)\) gián đoạn tại x = 2

(3) \(f(x)\)liên tục trên [-2;2]

A.Chỉ (1) và (3)       B. Chỉ (1)

C. Chỉ (2)                 D. Chỉ (2) và (3)

Câu 1: Tính \(\mathop {\lim }\limits_{x \to  - 2} \left( {3{x^2} - 3x - 8} \right)\)bằng?

A. -2.               B. 5.

C. 9.                D. 10.

Câu 2: Cho hàm số \(f(x) = \dfrac{{\sqrt x  - 1}}{{x - 1}}\). Tìm khẳng định đúng trong các khẳng định sau:

(I) \(f(x)\)gián đoạn tại x = 1.

(II) \(f(x)\)liên tục tại x = 1.

(III) \(\mathop {\lim }\limits_{x \to 1} f(x) = \dfrac{1}{2}\)

A.Chỉ (I)                  B. Chỉ (II)

C. Chỉ (I) và (III)     D. Chỉ (II) và (III)

Câu 3: Tìm khẳng định đúng trong các khẳng định sau:

I. \(f(x)\) liên tục trên đoạn [a;b] và \(f(a).f(b) < 0\) thì phương trình \(f(x) = 0\) có nghiệm.

II. \(f(x)\) không liên tục trên [a;b] và \(f(a).f(b) \ge 0\) thì phương trình \(f(x) = 0\) vô nghiệm.

A. Chỉ I đúng              B. Chỉ II đúng

C. Cả I và II đúng       D. Cả I và II sai

Câu 4: Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{\dfrac{{\sin 5x}}{{5x}}\,\,\,,x \ne 0}\\{a + 2\,\,\,,x = 0}\end{array}} \right.\). Tìm a để \(f(x)\)liên tục tại x = 0.

A.1                        B. -1

C. -2                      D. 2

Câu 5: Chọn giá trị \(f(0)\)để hàm số \(f(x) = \dfrac{{\sqrt {2x + 1}  - 1}}{{x(x + 1)}}\) liên tục tại x = 0.

A.1                        B. 2

C. 3                       D. 4

Câu 6: Tìm a để hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{\dfrac{{\sqrt {3x + 1}  - 2}}{{{x^2} - 1}}\,\,\,,khi\,x > 1}\\{\dfrac{{a({x^2} - 2)}}{{x - 3}}\,\,\,,khi\,x \le 1}\end{array}} \right.\) liên tục tại x = 1.

A. \(\dfrac{1}{2}\)                     B. \(\dfrac{1}{4}\)

C. \(\dfrac{3}{4}\)                     D. 1

Câu 7: Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{\dfrac{{3 - \sqrt {9 - x} }}{x}\,\,,0 < x < 9}\\{m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,x = 0}\\{\dfrac{3}{x}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,x \ge 9}\end{array}} \right.\,\,\). Tìm m để \(f(x)\)liên tục trên \({\rm{[}}0; + \infty )\) là:

A. \(\dfrac{1}{3}\)                         B. \(\dfrac{1}{2}\)

C. \(\dfrac{1}{6}\)                         D. 1

Câu 8: Cho hàm số \(f(x) = {x^3} - 1000{x^2} + 0,01\). Phương trình \(f(x) = 0\) có nghiệm thuộc khoảng nào trong các khoảng sau đây.

I.(-1;0)    , II. (0;1)    , III. ( 1;2).

A. Chỉ I                  B. Chỉ I và II

C. Chỉ II                 D. Chỉ III

Câu 9: Tính \(\mathop {\lim }\limits_{x \to 3} \dfrac{{{x^2} - 4x + 3}}{{{x^2} - 9}}\)bằng?

A. \(\dfrac{1}{5}.\)                      B. \(\dfrac{2}{5}.\)

C. \(\dfrac{1}{2}.\)                      D. \(\dfrac{1}{3}.\)

Câu 10: Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{\sqrt {\dfrac{{{x^2} + 1}}{{{x^3} - x + 6}}} \,\,\,\,\,;x \ne 3;x \ne 2}\\{b + \sqrt 3 \,\,\,\,\,\,;x = 3;b \in \mathbb{R}}\end{array}} \right.\). Tìm b để \(f(x)\)liên tục tại x = 3.

A. \(\sqrt 3 \)                      B. \( - \sqrt 3 \)

C. \(\dfrac{{2\sqrt 3 }}{3}\)                   D. \( - \dfrac{{2\sqrt 3 }}{3}\)