Câu 10 trang 135 SGK Đại số và Giải tích 11 Nâng cao

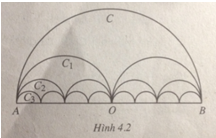
Gọi C là nửa đường tròn đường kính AB = 2R, C₁là đường gồm hai nửa đường tròn đường kính \({{AB} \over 2}\), C₂là đường gồm bốn nửa đường tròn đường kính \({{AB} \over 4},...\) C­_nlà đường gồm \({2^n}\) nửa đường tròn đường kính \({{AB} \over {{2^n}}},...\) (h. 4.2). Gọi p_n là độ dài của C_n, S_n là diện tích hình  phẳng giới hạn bởi  và đoạn thẳng AB.

a. Tính p_n và S_n.

b. Tìm giới hạn của các dãy số (p_n) và (S­_n).

a. Ta có:

\({p_n} = {2^n}.{R \over {{2^n}}}.\pi = \pi R\) với mọi n

\({S_n} = {2^n}.{\left( {{R \over {{2^n}}}} \right)^2}.{\pi \over 2} = {{\pi {R^2}} \over 2}.{1 \over {{2^n}}}\)

b.  \(\lim {p_n} = \pi R;\,\,\lim {S_n} = 0.\)