Câu C2 130 trang SGK Vật lý 12

I. PHẦN TRẮC NGHIỆM

Câu 1: Với những giá trị nào của \(x\) thì giá trị của các hàm số tương ứng sau bằng nhau \(y = \tan 3x\) và \(\tan (\dfrac{\pi }{3} - 2x)\) .          

A. \(x = \dfrac{\pi }{{15}} + k\dfrac{\pi }{5},\,k \in \mathbb{Z}\) 

B.  \(x = \dfrac{\pi }{{15}} + k\pi ,\,k \in \mathbb{Z}\)  

C. \(x = \dfrac{\pi }{{15}} + k\dfrac{\pi }{2},\,k \in \mathbb{Z}\)  

D. \(x = \dfrac{\pi }{5} + k\dfrac{\pi }{5},\,k \in \mathbb{Z}\)

Câu 2: Tìm m để phương trình \(\dfrac{{\cos x + 2\sin x + 3}}{{2\cos x - \sin x + 4}} = m\) có nghiệm.

A. \( - 3 \le m \le 2\)              B. \(m > 2\)

C. \(m \ge  - 3\)                     D. \(\dfrac{2}{{11}} \le m \le 2\)

Câu 3: Nghiệm của phương trình  \(\sin x + \sqrt 3 \cos x = \sqrt 2 \) là:

A. \(x =  - \dfrac{\pi }{{12}} + k2\pi ,\;x = \dfrac{{5\pi }}{{12}} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).\)

B. \(x =  - \dfrac{\pi }{4} + k2\pi ,\;x = \dfrac{{3\pi }}{4} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).\)

C. \(x = \dfrac{\pi }{3} + k2\pi ,\;x = \dfrac{{2\pi }}{3} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).\)

D. \(x =  - \dfrac{\pi }{4} + k2\pi ,\;x =  - \dfrac{{5\pi }}{4} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).\)

Câu 4 : Chọn mệnh đề đúng:

A. Hàm số \(y = \sin x\) có chu kỳ \(T = \pi \)

B. Hàm số \(y = \cos x\) và hàm số \(y = \tan x\) có cùng chu kỳ.

C. Hàm số \(y = \cot x\) và hàm số \(y = \tan x\) có cùng chu kỳ.

D. Hàm số \(y = \cot x\) có chu kỳ \(T = 2\pi \)

Câu 5: Nghiệm dương bé nhất của phương trình \(2{\sin ^2}x + 5\sin x - 3 = 0\)  là:

A. \(x = \dfrac{\pi }{3}.\)     B. \(x = \dfrac{\pi }{{12}}.\)

C. \(x = \dfrac{\pi }{6}.\)     D. \(x = \dfrac{{5\pi }}{6}.\)

Câu 6: Hàm số nào sau đây có đồ thị không là đường hình sin?

A. \(y = \sin x\)                        B. \(y = \cos x\)

C. \(y = \sin 2x\)                      D. \(y = \cot x\)

Câu 7: Tập xác định của hàm số\(y = f(x) = 2\cot (2x - \dfrac{\pi }{3}) + 1\) là:

A. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)   

B. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)

C. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + k\pi ,k \in \mathbb{Z}} \right\}\)     

D. \(\mathbb{R}\backslash \left\{ {\dfrac{{5\pi }}{{12}} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)

Câu 8: Nghiệm của phương trình \(\tan (x - \dfrac{\pi }{2}) = \sqrt 3 \) là:

A. \(x = \dfrac{{5\pi }}{6} + k\pi \).                            

B. \(x = \dfrac{{5\pi }}{6} + k2\pi \).                          

C. \(x = \dfrac{\pi }{6} + k2\pi \).                               

D. \(x = \dfrac{\pi }{6} + k\pi \).

Câu 9: Tập nghiệm của phương trình \(\cos 3x =  - 1\) là:

A. \(\left\{ { - \dfrac{\pi }{2} + k2\pi |k \in \mathbb{Z}} \right\}.\) 

B. \(\left\{ {\pi  + k2\pi |k \in \mathbb{Z}} \right\}.\)

C. \(\left\{ {\dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}|k \in \mathbb{Z}} \right\}.\)       

D. \(\left\{ {\dfrac{{k2\pi }}{3}|k \in \mathbb{Z}} \right\}.\)

Câu 10: Trong các hàm số sau, hàm số nào là hàm số chẵn.

A. \(y = \sin \left| {2016x} \right| + c{\rm{os}}2017x\).    

B. \(y = 2016\cos x + 2017\sin x\).

C. \(y = \cot 2015x - 2016\sin x\). 

D. \(y = \tan 2016x + \cot 2017x\).

Câu 11: Nghiệm của phương trình \(\sin 2x = \dfrac{{\sqrt 2 }}{2}\) là:

A.\(\,x = \dfrac{\pi }{8} + k2\pi ;x = \dfrac{{3\pi }}{8} + k2\pi (k \in Z)\)

B. \(\,x = \dfrac{\pi }{4} + k2\pi ;x = \dfrac{{3\pi }}{4} + k2\pi \,(k \in Z)\)

C.   \(\,x = \dfrac{\pi }{4} + k\pi ;x = \dfrac{{3\pi }}{4} + k\pi (k \in Z)\)

D. \(\,x = \dfrac{\pi }{8} + k\pi ;x = \dfrac{{3\pi }}{8} + k\pi ;k \in Z)\)

Câu 12: Giá trị nhỏ nhất m của hàm số \(y = 3\sin x + 1\) là.

A. m = 4                               B. m = -2 

C. m = 3                               D. m = 1

Câu 13: Tập xác định của hàm số \(y = f(x) = \dfrac{1}{{\sqrt {1 - sinx} }}\)

A. \(\mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\)        

B. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\)                 

C. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\)               

D. \(\phi \)

Câu 14: Giá trị nhỏ nhất của hàm số \(y = {\sin ^2}x - 4\sin x - 5\) là:

A. -9                                     B. 0

C. 9                                      D. -8

Câu 15: Đồ thị hàm số nào dưới đây nhận trục tung làm trục đối xứng?

A. \(y = \sin x - \cos x\).               

B. \(y = 2\sin x\).                          

C. \(y = 2\sin \left( { - x} \right)\).                                     

D. \(y =  - 2\cos x\)

Câu 16: Nghiệm của phương trình \(2{\sin ^2}x + \sin x\cos x - 3{\cos ^2}x = 0\) là.

A. \(x = \dfrac{\pi }{4} + k\pi \); \(x = \arctan ( - \dfrac{3}{2}) + k\pi ,k \in \mathbb{Z}\)

B. \(x = \dfrac{\pi }{4} + k\pi ,k \in \mathbb{Z}\)

C. \(x = \dfrac{\pi }{4} + k\pi \);\(x = \arctan ( - 3) + k\pi ,k \in \mathbb{Z}\)

D. \(x = \arctan ( - \dfrac{3}{2}) + k\pi ,k \in \mathbb{Z}\) 

Câu 17: Phương trình lượng giác nào dưới đây có nghiệm là: \(x = \dfrac{\pi }{6} + k\pi ,k \in \mathbb{Z}.\)

A. \(\cos 2x = \dfrac{{\sqrt 3 }}{2}.\)                          

B. \(\cot x = \sqrt 3 .\)    

C. \(\tan x = \sqrt 3 .\)     

D. \(\sin \left( {x - \dfrac{\pi }{3}} \right) =  - \dfrac{1}{2}\)

Câu 18: Giá trị lớn nhất M  của hàm số \(y = \sin x + \cos x\) là.

A. \(M = 2\)                         

B. \(M = 2\sqrt 2 \)             

C. \(M = 1\)                         

D. \(M = \sqrt 2 \)

Câu 19: Nghiệm của phương trình \(\sin x = \cos x\) là:

A. \(x = \dfrac{\pi }{4} + k2\pi \).                               

B. \(x = \dfrac{\pi }{4} + k\pi \).                                 

C. \(x = \dfrac{\pi }{4}\).    

D. \(x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\).

Câu 20: Đồ thì hình bên là đồ thị của hàm số nào?

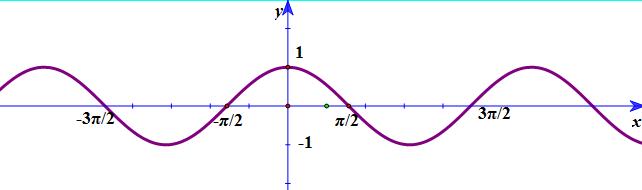
A. \(y = \sin x\)                     B. \(y = \cot x\)    

C. \(y = \tan x\)                    D. \(y = \cos x\)           

II. PHẦN TỰ LUẬN

Câu 21: Giải các phương trình sau

a) \(\sin 3x - \cos 2x = 0\)                                             

b) \(\dfrac{{\sin x + \sqrt 3 \cos x}}{{\sin x - \cos \dfrac{\pi }{4}}} = 0\)

Câu 22: Giải phương trình :   \(2{\cos ^2}\left( {\dfrac{\pi }{4} - 2x} \right) + \sqrt 3 \cos 4x = 4{\cos ^2}x - 1\)

I. PHẦN TRẮC NGHIỆM

Câu 1: Tập xác định của hàm số: \(y = \dfrac{1}{{\sqrt {1 - cos3x} }}\) là:

A.\(\left\{ {k\dfrac{\pi }{3};k \in \mathbb{Z}} \right\}\)

\(B.\mathbb{R}\backslash \left\{ {k\dfrac{{2\pi }}{3};k \in \mathbb{Z}} \right\}\)          

\(C.\left\{ {\dfrac{{k2\pi }}{3};k \in \mathbb{Z}} \right\}\)

D. \(\mathbb{R}\backslash \left\{ {\dfrac{{k\pi }}{3};k \in \mathbb{Z}} \right\}\)

Câu 2: Tập giá trị của hàm số \(y = 2\sqrt 3 \sin 2x - 2cos2x\) là:

 A. [-1; 1]            B. [-2; 2]                             

C. [-3; 3]             D. [-4; 4]

Câu 3: Phương trình \(2\sin \left( {2x + \dfrac{\pi }{4}} \right) = 1\) có các họ nghiệm là:

A. \(x =  - \dfrac{\pi }{{12}} + k2\pi ;\,k \in \mathbb{Z}\)

B. \(x = \dfrac{{7\pi }}{{12}} + k2\pi ;\,k \in \mathbb{Z}\)             

C. Cả A và B 

D. Đáp án khác

Câu 4: Hàm số \(y = cos2x\, - \,{\sin ^2}x\) là:

A. Hàm số chẵn

B. Hàm số lẻ                          

C. Hàm số không chẵn, không lẻ

D. Hàm số vừa chẵn, vừa lẻ

Câu 5: Phương trình \(\cot \left( {2x + \dfrac{\pi }{3}} \right) + 1 = 0\) có các họ nghiệm là:

\(A.\,x =  - \dfrac{{7\pi }}{{24}} + k\pi ,k \in \mathbb{Z}\)

\(B.\,x = \dfrac{{7\pi }}{{24}} + k\pi ,\,k \in \mathbb{Z}\)              

\(C.\,x = \dfrac{\pi }{{24}} + k\dfrac{\pi }{2};\,k \in \mathbb{Z}\)

D. \(x = \dfrac{{ - 7\pi }}{{24}} + k\dfrac{\pi }{2};k \in \mathbb{Z}\)

Câu 6: Phương trình \(2co{s^2}2x\, + \,\left( {\sqrt 3  - 2} \right)cos2x\, - \sqrt 3  = 0\) có các họ nghiệm là:

\(A.\,x = k2\pi ,\,x = \dfrac{{ - 5\pi }}{6} + k\pi ,\,x = \dfrac{{5\pi }}{6} + k2\pi ;\,k \in \mathbb{Z}\)

B. \(x = k\pi ; \pm \dfrac{{5\pi }}{{12}} + k\pi ;k \in \mathbb{Z}\)

\(C.\,x = k\pi ;\,x = \dfrac{{5\pi }}{{12}} + k\pi ;\,k \in \mathbb{Z}\)

D. \(x = \dfrac{{ - 5\pi }}{{12}} + k\dfrac{\pi }{2};k \in \mathbb{Z}\)

Câu 7: Phương trình \(\sqrt 2 {\mathop{\rm sinx}\nolimits}  - \sqrt 2 \cos x = \sqrt 3 \) có các họ nghiệm là:

\(\begin{array}{l}A.\,x = \dfrac{{7\pi }}{{12}} + k2\pi ;\,x = \dfrac{{11\pi }}{{12}} + k\pi ,\,k \in \mathbb{Z}\\B.\,x = \dfrac{{5\pi }}{{12}} + k2\pi ,\,x = \dfrac{{11\pi }}{{12}} + k2\pi ;\,k \in \mathbb{Z}\end{array}\)

C. \(x = \dfrac{{7\pi }}{{12}} + k2\pi ;x = \dfrac{{11\pi }}{{12}} + k2\pi ;k \in \mathbb{Z}\)

\(D.\,x = \dfrac{{7\pi }}{{12}} + k\pi ;\,x = \dfrac{{11\pi }}{{12}} + k\pi ;\,k \in \mathbb{Z}\)

Câu 8: Tổng các nghiệm thuộc đoạn  \(\left[ { - \pi ;\pi } \right]\)của phương trình \(\cos 5x + \cos x = \sin 2x - \sin 4x\)là:

A. 0                                         B. \(2\pi \)

C. \(4\pi \)                                D. \(6\pi \)

Câu 9: Giá trị nhỏ nhất của hàm số \(y = \dfrac{{\sin x + 2\cos x + 1}}{{\cos x - 3\sin x + 4}}\) là:

A. \(2\)            B.\( - \dfrac{1}{3}\)

C. \(\dfrac{{ - 1}}{2}\)            D. 1

Câu 10: Phương trình \(3{\sin ^2}x - 7\sin x\cos x - 10{\cos ^2}x = 0\) có các họ nghiệm là:

A. \(x = \dfrac{{ - \pi }}{4} + k2\pi ;x = \arctan \dfrac{{10}}{3} + k2\pi ;k \in \mathbb{Z}\)

B. \(x = \dfrac{{ - \pi }}{4} + k\pi ;x = \arctan \dfrac{7}{2} + k2\pi ;k \in \mathbb{Z}\)

C.\(x = \dfrac{{ - \pi }}{4} + k\pi ;x = \arctan \dfrac{{10}}{3} + k\pi ;k \in \mathbb{Z}\)

D. \(x = \dfrac{{ - \pi }}{4} + k2\pi ;x = \arctan \dfrac{{10}}{3} + k\pi ;k \in \mathbb{Z}\)

Câu 11: Phương trình \(2\sin x = \sqrt 2 \) có bao nhiêu nghiệm thuộc \(\left( {\pi ;6\pi } \right)\):

A.3                                          B.5

C.4                                          D.6

Câu 12: Tổng tất cả các giá trị nguyên của m để phương trình \(\left( {m + 1} \right)\sin x - 2m\cos x + 2m - 1 = 0\) vô nghiệm là:

 A. 15                          B. -15

C. 14                           D. -14

Câu 13: Có bao nhiêu giá trị nguyên của m để phương trình \(\left( {2m + 1} \right)\cos x + m - 1 = 0\) vô nghiệm .

A. 15                           B. 2

C. 3                             D. 1

Câu 14: Tìm m để phương trình \(\cos 2x - \cos x - m = 0\) có nghiệm.

A. \(\dfrac{{ - 9}}{8} \le m \le 2\)

B. \(\dfrac{{ - 9}}{8} \le m \le 1\)

C. \(m \ge \dfrac{{ - 9}}{8}\)

D. \(\dfrac{{ - 5}}{8} \le m \le 2\)

Câu 15: Phương trình \(\sqrt 3 {\cot ^2}x - 4\cot x + \sqrt 3  = 0\) có nghiệm là:

A. \(\left[ \begin{array}{l}x = \dfrac{\pi }{3} + k\pi \\x = \dfrac{\pi }{6} + k\pi \end{array} \right.\,\,\left( {k \in Z} \right)\)

B. \(\left[ \begin{array}{l}x = \dfrac{\pi }{3} + k2\pi \\x = \dfrac{\pi }{6} + k2\pi \end{array} \right.\,\,\left( {k \in Z} \right)\)

C. \(\left[ \begin{array}{l}x =  - \dfrac{\pi }{3} + k\pi \\x =  - \dfrac{\pi }{6} + k\pi \end{array} \right.\,\,\left( {k \in Z} \right)\)

D. \(\left[ \begin{array}{l}x =  - \dfrac{\pi }{3} + k2\pi \\x = \dfrac{\pi }{6} + k\pi \end{array} \right.\,\,\left( {k \in Z} \right)\)

Câu 16: Cho phương trình \(cos3x – 4 cos2x + 3cos x – 4 = 0\) có bao nhiêu nghiệm trên [0; 14]?

A. 3.                                        B. 4

C. 5                                         D. 6

Câu 17: Tập xác định của hàm số \(y = 2016{\tan ^{2017}}2x\) là

A. \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).

B. \(D = \mathbb{R}\backslash \left\{ {k\dfrac{\pi }{2}\left| {k \in \mathbb{Z}} \right.} \right\}\).               

C. \(D = \mathbb{R}\).

D.  \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{4} + k\dfrac{\pi }{2}\left| {k \in \mathbb{Z}} \right.} \right\}\).

Câu 18: Cho hai hàm số \(f\left( x \right) = \dfrac{1}{{x - 3}} + 3{\sin ^2}x\) và \(g\left( x \right) = \sin \sqrt {1 - x} \). Kết luận nào sau đây đúng về tính chẵn lẻ của hai hàm số này?

A. Hai hàm số \(f\left( x \right);g\left( x \right)\) là hai hàm số lẻ.

B. Hàm số \(f\left( x \right)\) là hàm số chẵn; hàm số \(f\left( x \right)\) là hàm số lẻ.

C. Hàm số \(f\left( x \right)\) là hàm số lẻ; hàm số \(g\left( x \right)\) là hàm số không chẵn không lẻ.

D. Cả hai hàm số \(f\left( x \right);g\left( x \right)\) đều là hàm số không chẵn không lẻ.

Câu 19: Phương trình \(1 + \sin \,x\, - \,cos\,x - \sin 2x = 0\) có bao nhiêu nghiệm trên \(\left[ {0;\,\dfrac{\pi }{2}} \right)\)?

A. 1 .                                       B. 2 .

C. 3 .                                       D. 4.

Câu 20: Giải phương trình  \({\cos ^3}x - {\sin ^3}x = \cos 2x\)

A. \(x = k2\pi ,x = \dfrac{\pi }{2} + k2\pi ,x = \dfrac{\pi }{4} + k2\pi \).

B. \(x = k2\pi ,x = \dfrac{\pi }{2} + k2\pi ,x = \dfrac{\pi }{4} + k\pi \).

C. \(x = k\pi ,x = \dfrac{\pi }{2} + k\pi ,x = \dfrac{\pi }{4} + k\pi \).

D. \(x = k2\pi ,x = \dfrac{\pi }{2} + k\pi ,x = \dfrac{\pi }{4} + k\pi \).

II. PHẦN TỰ LUẬN

Câu 21: Giải các phương trình sau

a) \(\sqrt 3 \sin 3x + \cos 3x =  - 1\)

b) \(\cos x\cos 5x = \dfrac{1}{2}\cos 6x\)

Câu 22: Giải phương trình sau:

\(2\sin x(1 + \cos 2x) + \sin 2x = 1 + 2\cos x\)  

I. PHẦN TRẮC NGHIỆM

Câu 1: Hàm số \(y = \sin 3x.\cos x\)là một hàm số tuần hoàn có chu kì là

A. \(\pi \)                            B. \(\dfrac{\pi }{4}\)

C. \(\dfrac{\pi }{3}\)                           D. \(\dfrac{\pi }{2}\)

Câu 2: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số \(y = {\sin ^4}x - 2{\cos ^2}x + 1\)

A. M = 2, m = -2          

B. M = 1,  m = 0

C. M = 4, m = -1                    

D. M = 2, m = -1

Câu 3: Tập xác định của hàm số \(y = \sqrt {1 - \cos 2017x} \) là

A. \(D = \mathbb{R}\backslash \left\{ {k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).   

B. \(D = \mathbb{R}\).                        

C. \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{4} + k\pi ;\,\dfrac{\pi }{2} + k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).

D.  \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).

Câu 4: Tìm chu kì T của hàm số \(y = \cot 3x + \tan x\) là

A. \(\pi \)                                 B. \(3\pi \)

C. \(\dfrac{\pi }{3}\)                               D. \(4\pi \)

Câu 5: Cho hàm số \(f\left( x \right) = \left| x \right|sinx.\) Phát biểu nào sau đây là đúng về hàm số đã cho?

A. Hàm số đã cho có tập xác định \(D = \mathbb{R}\backslash \left\{ 0 \right\}.\)            

B. Đồ thị hàm số đã cho có tâm đối xứng.                           

C. Đồ thị hàm số đã cho có trục xứng.                                 

D. Hàm số có tập giá trị là \(\left[ { - 1;\,1} \right].\)

Câu 6: Trong các phương trình sau đây,phương trình nào có tập nghiệm là \(x =  - \dfrac{\pi }{3} + k2\pi \) và \(x = \dfrac{{4\pi }}{3} + k2\pi ,\,\,\,(k \in \mathbb{Z})\)

A. \(\sin \,x = \dfrac{2}{{\sqrt 2 }}\)

B. \(\sin \,x = \dfrac{1}{{\sqrt 2 }}\)

C. \(\sin \,x =  - \dfrac{{\sqrt 3 }}{2}\)

D. \(\sin \,x = \dfrac{{\sqrt 2 }}{{\sqrt 3 }}\)

Câu 7: Phương trình \(\tan \left( {3x - {{15}^0}} \right) = \sqrt 3 \) có các nghiệm là:

A. \(x = {60^0} + k{180^0}\)

B. \(x = {75^0} + k{180^0}\)

C. \(x = {75^0} + k{60^0}\)

D. \(x = {25^0} + k{60^0}\)

Câu 8: Nghiệm âm lớn nhất của phương trình \(\dfrac{{\sqrt 3 }}{{{{\sin }^2}\,x}} = 3\cot \, + \,\sqrt 3 \) là:

A. \( - \dfrac{\pi }{2}\)                               B. \( - \dfrac{{5\pi }}{6}\)

C. \( - \dfrac{\pi }{6}\)                               D. \( - \dfrac{{2\pi }}{3}\)

Câu 9: Phương trình \(sin x + cos x – 1 = 2sin xcos x\) có bao nhiêu nghiệm trên \(\left[ {0;\,2\pi } \right]\) ?

A. 2.                       B. 3.

C. 4.                       D. 6.

Câu 10: Phương trình \(\sin (x + {10^0}) = \dfrac{1}{2}\,\,({0^0} < x < {180^0})\)có nghiệm là:

A. \(x = {30^0}\) và \(x = {150^0}\)

B. \(x = {20^0}\) và \(x = {140^0}\)

C. \(x = {40^0}\) và \(x = {160^0}\)

D. \(x = {30^0}\) và\(\,x = {140^0}\)

Câu 11: Phương trình \(\sin (5x + \dfrac{\pi }{2}) = m - 2\) có nghiệm khi:

A. \(m \in \left[ {1;3} \right]\)

B. \(m \in \left[ { - 1;1} \right]\)

C. \(m \in R\)

D. \(m \in (1;3)\)

Câu 12: Phương trình nào sau đây tương đương với phương trình \(\cos x = 0\)?

A. \({\mathop{\rm s}\nolimits} {\rm{inx}} = 1\)

B. \({\mathop{\rm s}\nolimits} {\rm{inx}} =  - 1\)

C. \({\mathop{\rm t}\nolimits} {\rm{anx}} = 0\)

D. \(\cot x = 0\)

Câu 13: Phương trình \(m\tan x - \sqrt 3  = 0\) Có nghiệm khi

A. \(m \ne 0\).

B. \(m \in R\)

C. \( - 1 \le \dfrac{{\sqrt 3 }}{m} \le 1\)

D. \( - 1 < \dfrac{{\sqrt 3 }}{m} < 1\)

Câu 14: Phương trình \(\sin x + m\cos x = \sqrt {10} \) có nghiệm khi:

A. \(\left[ \begin{array}{l}m \ge 3\\m \le  - 3\end{array} \right.\).

B. \(\left[ \begin{array}{l}m > 3\\m <  - 3\end{array} \right.\).

C. \(\left[ \begin{array}{l}m \ge 3\\m <  - 3\end{array} \right.\).

D. \( - 3 \le m \le 3\).

Câu 15: Phương trình \({\rm{cos}}2x + \sin x = \sqrt 3 \left( {\cos x - \sin 2x} \right)\) có các nghiệm là:

A. \(\left[ \begin{array}{l}x = \dfrac{\pi }{{18}} + k\dfrac{{2\pi }}{3}\\x =  - \dfrac{{3\pi }}{2} - k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).

B. \(\left[ \begin{array}{l}x =  - \dfrac{\pi }{4} + k\pi \\x =  - \dfrac{\pi }{{12}} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).

C. \(\left[ \begin{array}{l}x = \dfrac{\pi }{{12}} + k\pi \\x = \dfrac{\pi }{4} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).

D. \(\left[ \begin{array}{l}x = \dfrac{\pi }{{12}} + k2\pi \\x =  - \dfrac{\pi }{4} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).

Câu 16: Phương trình \(\sin 5x.\cos 3x = \sin 7x.\cos 5x\) có tập nghiệm là:

A. \(\left[ \begin{array}{l}x = k\dfrac{\pi }{2}\\x = \dfrac{\pi }{{20}} + k\dfrac{\pi }{{10}}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\).

B. \(\left[ \begin{array}{l}x = k\pi \\x = \dfrac{\pi }{{20}} + k\dfrac{\pi }{{10}}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\).

C. \(\left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\dfrac{\pi }{{10}}\\x = \dfrac{\pi }{{20}} + k\dfrac{\pi }{{10}}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\).

D. \(\left[ \begin{array}{l}x = k\dfrac{\pi }{2}\\x = \dfrac{\pi }{{20}} + k\dfrac{\pi }{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\).

Câu 17: Các giá trị của \(m \in \left[ {a;b} \right]\) để phương trình \(\cos 2x + {\sin ^2}x + 3\cos x - m = 5\) có nghiệm thì:

A. \(a + b = 2\).                               

B. \(a + b = 12\).

C. \(a + b =  - 8\).                            

D. \(a + b = 8\).

Câu 18: Chọn mệnh đề đúng:

A. \(\cos x \ne 1 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\)

B. \(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\)

C. \(\cos x \ne  - 1 \Leftrightarrow x \ne  - \dfrac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\)

D. \(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\)

Câu 19: Nghiệm của phương trình \(\tan 4x.\cot 2x = 1\) là:

A. \(k\pi ,k \in \mathbb{Z}\)

B. \(\dfrac{\pi }{4} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}\)

C. \(\dfrac{{k\pi }}{2},k \in \mathbb{Z}\)

D. Vô nghiệm

Câu 20: Nghiệm của phương trình \(\cos 3x = \cos x\) là:

A. \(k2\pi \left( {k \in \mathbb{Z}} \right)\)

B. \(k2\pi ;\dfrac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\)

C. \(\dfrac{{k\pi }}{2}\left( {k \in \mathbb{Z}} \right)\)

D. \(k\pi ;\dfrac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\)

II. PHẦN TỰ LUẬN

Câu 21: Giải các phương trình sau

\(a)  3{\sin ^2}2x + 7\cos 2x - 3 = 0\)

\(b)  {\sin ^2}2x + c{\rm{o}}{{\rm{s}}^{\rm{2}}}x = 1\)

Câu 22: Giải phương trình sau:

\(\cos 2x + 3\sin 2x + 5\sin x - 3\cos x = 3\)  

I. PHẦN TRẮC NGHIỆM

Câu 1: Giải phương trình \({\tan ^2}3x - 1 = 0\).

A. \(x =  \pm \dfrac{\pi }{4} + k\pi \)

B. \(x =  \pm \dfrac{\pi }{{12}} + k\pi \)

C. \(x =  \pm \dfrac{\pi }{8} + k\dfrac{\pi }{2}\)

D. \(x =  \pm \dfrac{\pi }{{12}} + k\dfrac{\pi }{3}\)

Câu 2: Tìm tập xác định \(D\) của hàm số \(y = \dfrac{{1 - 4\sin x}}{{\cos x}}\).

A. \(D = \mathbb{R}\backslash \left\{ {k\pi ,\,\,k \in \mathbb{Z}} \right\}\)

B. \(D = \mathbb{R}\backslash \left\{ {k2\pi ,\,\,k \in \mathbb{Z}} \right\}\)

C. \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)

D. \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}\)

Câu 3: Tính giá trị biểu thức \(P = {\sin ^2}{45^0} - \cos {60^0}\).

A. \(P = 0\)                           B. \(P = \dfrac{1}{2}\)

C. \(P = 1\)                           D. \(P =  - 1\)

Câu 4: Giải phương trình \({\mathop{\rm s}\nolimits} {\rm{in2}}x - \cos 2x =  - \sqrt 2 \).

A. \(x =  - \dfrac{\pi }{4} + k2\pi \)

B. \(x = \dfrac{{3\pi }}{8} + k\pi \)

C. \(x =  - \dfrac{\pi }{8} + k\pi \)

D. \(x = \dfrac{\pi }{4} + k\pi \)

Câu 5: Phương trình nào sau đây có nghiệm?

A. \(5\sin x - 2\cos x = 3\)   

B. \(\sin x + \cos x = 2\)       

C. \(\sin x - 4\cos x =  - 5\)  

D. \(\cos x + \sqrt 3 \sin x = 3\)

Câu 6: Tìm giá trị lớn nhất \(M\) của hàm số \(y = 7\cos 5x - 1\).

A. \(M = 7\)                          B. \(M = 5\)

C. \(M = 6\)                          D. M = 8

Câu 7: Phương trình nào sau đây vô nghiệm?

A. \(9 - \cot x = 0\)              

B. \(2\tan x + 9 = 0\)

C. \(1 - 4\sin x = 0\)             

D. \(5 + 4\cos x = 0\)

Câu 8: Giải phương trình \(\sqrt 3 \sin x + \cos x = 1\).

A. \(x = k2\pi ;\,\,x = \dfrac{{2\pi }}{3} + k2\pi \)

B. \(x =  - \dfrac{\pi }{3} + k2\pi ;\,\,x = \dfrac{{4\pi }}{3} + k2\pi \)

C. \(x =  - \dfrac{\pi }{6} + k2\pi ;\,\,x = \dfrac{\pi }{2} + k2\pi \)

D. \(x = \dfrac{\pi }{6} + k2\pi ;\,\,x = \dfrac{{5\pi }}{6} + k2\pi \)

Câu 9: Hàm số nào sau đây là hàm số chẵn.

A. \(y = \sin x\)                     B. \(y = \cos x\)

C. \(y = \cot x\)                     D. \(y = \tan x\)

Câu 10: Giải phương trình \(2{\sin ^2}x - 3\sin x - 2 = 0\).

A. \(x =  - \dfrac{\pi }{3} + k2\pi ;\,\,\,x = \dfrac{{4\pi }}{3} + k2\pi \)

B. \(x = \dfrac{\pi }{6} + k2\pi ;\,\,\,x = \dfrac{{5\pi }}{6} + k2\pi \)

C. \(x =  - \dfrac{\pi }{6} + k2\pi ;\,\,\,x = \dfrac{{7\pi }}{6} + k2\pi \)

D. \(x = \dfrac{\pi }{3} + k2\pi ;\,\,\,x = \dfrac{{2\pi }}{3} + k2\pi \)

Câu 11: Giải phương trình  \(\tan \left( {2x} \right) = \tan {\rm{8}}{0^0}\).

A. \(x = {40^0} + k{180^0}\)

B. \(x = {40^0} + k{90^0}\)

C. \(x = {40^0} + k{45^0}\)

D. \(x = {80^0} + k{180^0}\)

Câu 12: Giải phương trình \(1 + \cos x = 0\).

A. \(x = \dfrac{\pi }{2} + k2\pi \)

B. \(x = \pi  + k2\pi \)

C. \(x = \dfrac{\pi }{2} + k\pi \)

D. \(x = k2\pi \)

Câu 13: Giải phương trình \(\sin 6x - \cos 4x = 0\).

A. \(x = \dfrac{\pi }{{20}} + k\dfrac{\pi }{5};\,x = \dfrac{\pi }{4} + k\pi \)

B. \(x = \dfrac{\pi }{{20}} + k\dfrac{\pi }{5};\,x = \dfrac{\pi }{4} + k\dfrac{\pi }{2}\)

C. \(x = \dfrac{\pi }{4} + k\pi ;\,x = \dfrac{\pi }{{20}} + k\dfrac{{2\pi }}{5}\)

D. \(x = k\pi ;\,x = \dfrac{\pi }{{10}} + k\dfrac{\pi }{5}\)

Câu 14: Giải phương trình \(1 - 2\sin x = 0\).

A. \(\left\{ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\)

B. \(\left[ \begin{array}{l}x =  - \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{7\pi }}{6} + k2\pi \end{array} \right.\)

C. \(\left\{ \begin{array}{l}x =  - \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{7\pi }}{6} + k2\pi \end{array} \right.\)

D. \(\left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\)

Câu 15: Cho phương trình \(\cos 4x = 3m - 5\). Tìm \(m\) để phương trình đã cho có nghiệm.

A. \( - 1 \le m \le 1\)              B. \(\dfrac{4}{3} \le m \le 2\)

C. \( - 2 \le m \le \dfrac{4}{3}\)         D. \(\dfrac{4}{3} \le m \le 3\)

Câu 16: Cho phương trình \(2\cos 4x - {\rm{sin4}}x = m\) . Tìm tất cả các giá trị của \(m\) để phương trình đã cho có nghiệm.

A. \( - \sqrt 3  \le m \le \sqrt 3 \)

B. \(m \le  - \sqrt 3 ;\,\,m \ge \sqrt 3 \)                         

C. \( - \sqrt 5  \le m \le \sqrt 5 \)

D. \(m \le  - \sqrt 5 ;\,\,m \ge \sqrt 5 \)

Câu 17: Giải phương trình \({\mathop{\rm s}\nolimits} {\rm{in3}}x + \sqrt 3 \cos 3x = 2\sin x\)

A. \(\left[ \begin{array}{l}x =  - \dfrac{\pi }{{12}} + k\pi \\x = \dfrac{{5\pi }}{{12}} + k\pi \end{array} \right.\)

B. \(\left[ \begin{array}{l}x =  - \dfrac{\pi }{6} + k\pi \\x = \dfrac{\pi }{6} + k\dfrac{\pi }{2}\end{array} \right.\)

C. \(\left[ \begin{array}{l}x =  - \dfrac{\pi }{6} + k\pi \\x = \dfrac{\pi }{3} + k\pi \end{array} \right.\)

D. \(\left[ \begin{array}{l}x =  - \dfrac{\pi }{{12}} + k\pi \\x = \dfrac{{5\pi }}{{24}} + k\dfrac{\pi }{2}\end{array} \right.\)

Câu 18: Giải phương trình \({\rm{sin3}}x - \sin x = 0\).

A. \(\left[ \begin{array}{l}x = k\pi \\x = \dfrac{\pi }{4} + k\pi \end{array} \right.\)

B. \(\left[ \begin{array}{l}x = k\pi \\x = \dfrac{\pi }{2} + k\pi \end{array} \right.\)

C. \(\left[ \begin{array}{l}x = k\dfrac{\pi }{2}\\x = \dfrac{\pi }{2} + k\pi \end{array} \right.\)

D. \(\left[ \begin{array}{l}x = k\pi \\x = \dfrac{\pi }{4} + k\dfrac{\pi }{2}\end{array} \right.\)

Câu 19: Tìm giá trị nhỏ nhất \(m\) của hàm số \(y = {\sin ^2}x - 4{\cos ^2}x + 9\).

A. \(m = \dfrac{{15}}{2}\)   B. \(m = 5\)

C. \(m =  - \dfrac{5}{2}\)     D. \(m =  - 5\)

Câu 20: Hàm số nào sau đây xác định với mọi \(x \in \mathbb{R}\).

A. \(y = 7 - 4\tan x\)             B. \(y = \dfrac{7}{{{{\sin }^2}x}}\)

C. \(y = \dfrac{{\sin x + 1}}{{3 - \cos x}}\)                  D. \(y = \cot x\)

II. PHẦN TỰ LUẬN

Câu 21: Giải các phương trình sau

\(a) \, \sin 3x = \cos x\)

\(b) \, 2{\sin ^2}x + \sqrt 3 \sin 2x = 2\)

Câu 22: Giải phương trình sau:

\(2\sin x + \cos x - \sin 2x - 1 = 0\)  

I. PHẦN TRẮC NGHIỆM

Câu 1: Tập xác định của hàm số \(y = \dfrac{{1 - \sin x}}{{\sin x + 1}}\) là:

A. \(x \ne \dfrac{\pi }{2} + k2\pi \)                             

B. \(x \ne k2\pi \)

C. \(x \ne \dfrac{{3\pi }}{2} + k2\pi \)                        

D. \(x \ne \pi  + k2\pi \)

Câu 2:Hàm số \(y=\sin x\) xác định trên:

A. \(\mathbb R\backslash \left\{ {k\pi ,k \in Z} \right\}\)     

B. \(\mathbb R\)

C. \(\mathbb R\backslash \left\{ {{{k\pi } \over 2},k \in Z} \right\}\)           

D. \([4;3]\)

Câu 3: Cho phương trình: \(\sqrt 3 \cos x + m - 1 = 0\) . Với giá trị nào của m thì phương trình có nghiệm

A. \(m < 1 - \sqrt 3 \)

B. \(m > 1 + \sqrt 3 \)

C. \(1 - \sqrt 3  \le m \le 1 + \sqrt 3 \)

D. \( - \sqrt 3  \le m \le \sqrt 3 \)

Câu 4: Cho biết \(\,x =  \pm \dfrac{{2\pi }}{3} + k2\pi \) là họ nghiệm của phương trình nào sau đây?

A. \(2\cos x - 1 = 0\)            

B. \(2\cos x + 1 = 0\)

C. \(2\sin x + 1 = 0\)            

D. \(2\sin x - \sqrt 3  = 0\)

 Câu 5: Nghiệm của phương trình \(\sin 3x = \cos x\)  là:

A. \(\,x = \dfrac{\pi }{8} + k\dfrac{\pi }{2};\,\,x = \dfrac{\pi }{4} + k\pi \)

B. \(x = k2\pi ;\,\,x = \dfrac{\pi }{2} + k2\pi \)

C. \(x = k\pi ;\,\,x = \dfrac{\pi }{4} + k\pi \)

D. \(x = k\pi ;\,\,x = k\dfrac{\pi }{2}\)

Câu 6: Số nghiệm của phương trình \(2\cos x + \sqrt 2  = 0\) trên khoảng \(\left( { - 6;6} \right)\) là:

A. \(4\)                                  B. \(6\)

C. \(5\)                                  D. \(3\)

Câu 7: Hàm số nào sau đây không phải là hàm số chẵn, cũng không phải là hàm số lẻ.

A. \(y = {x^2} - {\mathop{\rm s}\nolimits} {\rm{in4}}x\)

B. \(y = \dfrac{{\sin x - \cot x}}{x}\)

C. \(y = {x^4} - \cos x\)

D. \(y = {x^2}\tan x\)

Câu 8: Giải phương trình \(\cos 2x - \sqrt 3 \sin x = 1\).

A. \(x = k\pi ;\,\,x =  - \dfrac{\pi }{6} + k2\pi ;\,\,x = \dfrac{{7\pi }}{6} + k2\pi \)

B. \(x = k2\pi ;\,\,x =  - \dfrac{{2\pi }}{3} + k2\pi \)

C. \(x = k\pi ;\,\,x =  - \dfrac{\pi }{3} + k2\pi ;\,\,x = \dfrac{{4\pi }}{3} + k2\pi \)

D. \(x = k\pi ;\,\,x = \dfrac{\pi }{3} + k2\pi ;\,\,x = \dfrac{{2\pi }}{3} + k2\pi \)

Câu 9: Giải phương trình \(\cos 2x + \sin 2x = \sqrt 2 \cos x\) .

A. \(\left[ \begin{array}{l}x = \dfrac{\pi }{4} + k\dfrac{{2\pi }}{3}\\x = \dfrac{{3\pi }}{4} + k2\pi \end{array} \right.\)

B. \(\left[ \begin{array}{l}x =  - \dfrac{\pi }{4} + k2\pi \\x =  - \dfrac{\pi }{{12}} + k\dfrac{{2\pi }}{3}\end{array} \right.\)

C. \(\left[ \begin{array}{l}x = \dfrac{\pi }{4} + k2\pi \\x = \dfrac{{4\pi }}{9} + k\dfrac{{2\pi }}{3}\end{array} \right.\)

D. \(\left[ \begin{array}{l}x = \dfrac{\pi }{4} + k2\pi \\x = \dfrac{\pi }{{12}} + k\dfrac{{2\pi }}{3}\end{array} \right.\)

Câu 10: Giải phương trình \(\cos 4x - \sqrt 3 {\mathop{\rm s}\nolimits} {\rm{in4}}x = 0\).

A. \(x = \dfrac{\pi }{{12}} + k\dfrac{\pi }{4}\)

B. \(x = \dfrac{\pi }{8} + k\dfrac{\pi }{4}\)

C. \(x = k\dfrac{\pi }{4}\)

D. \(x = \dfrac{\pi }{{24}} + k\dfrac{\pi }{4}\)

Câu 11: Giải phương trình \({\sin ^2}x - \cos x - 1 = 0\).

A. \(x = k\pi ;\,\,x = \dfrac{\pi }{2} + k2\pi \)

B. \(x = \dfrac{\pi }{2} + k2\pi ;\,\,x =  - \dfrac{\pi }{2} + k2\pi \)

C. \(x = \dfrac{\pi }{2} + k\pi ;\,\,x = \pi  + k2\pi \)

D. \(x = k\pi ;\,\,x =  - \dfrac{\pi }{2} + k2\pi \)

Câu 12: Giải phương trình \(\cos x - \sin x =  - \dfrac{{\sqrt 6 }}{2}\).

A. \(x =  - \dfrac{\pi }{{12}} - k2\pi ;\,\,x = \dfrac{{19\pi }}{{12}} - k2\pi \)

B. \(x = \dfrac{{7\pi }}{{12}} + k2\pi ;\,\,x =  - \dfrac{{13\pi }}{{12}} + k2\pi \)

C. \(x = \dfrac{\pi }{{12}} + k2\pi ;\,\,x = \dfrac{{19\pi }}{{12}} + k2\pi \)

D. \(x =  - \dfrac{{7\pi }}{{12}} - k2\pi ;\,\,x = \dfrac{{13\pi }}{{12}} - k2\pi \)

Câu 13: Mệnh đề nào sau đây sai?

A. Hàm số \(y = \sin x\) tăng trong khoảng \(\left( {0;\dfrac{\pi }{2}} \right)\)

B. Hàm số \(y = \cot x\) giảm trong khoảng \(\left( {0;\dfrac{\pi }{2}} \right)\)

C. Hàm số \(y = \tan x\) tăng trong khoảng \(\left( {0;\dfrac{\pi }{2}} \right)\)

D. Hàm số \(y = \cos x\) tăng trong khoảng \(\left( {0;\dfrac{\pi }{2}} \right)\)

Câu 14: GTNN và GTLN của hàm số \(y = 4\sqrt {\sin x + 3}  - 1\) lần lượt là

A. \(\sqrt 2 ;\,2\)              B. \(2;\,4\)                       

C. \(4\sqrt 2 ;\,\,8\)          D. \(4\sqrt 2  - 1;\,\,7\) 

Câu 15: Nghiệm đặc biệt nào sau đây là sai

A. \(\sin x =  - 1 \Leftrightarrow x = \dfrac{{ - \pi }}{2} + k2\pi \)

B. \(\sin x = 0 \Leftrightarrow x = k\pi \)

C. \(\sin x = 0 \Leftrightarrow x = k2\pi \)

D. \(\sin x = 1 \Leftrightarrow x = \dfrac{\pi }{2} + k2\pi \)

Câu 16: Số nghiệm của phương trình \(\sin 2x = \dfrac{{\sqrt 3 }}{2}\)trong \(\left( {0;3\pi } \right)\)là

A. \(1\)                                     B. \(2\)

C. \(6\)                                     D. \(4\)

Câu 17: Tìm tổng các nghiệm của phương trình \(2\cos \left( {x - \dfrac{\pi }{3}} \right) = 1\) trên \(\left( { - \pi ;\pi } \right)\)

A. \(\dfrac{{2\pi }}{3}\)                      B. \(\dfrac{\pi }{3}\)

C. \(\dfrac{{4\pi }}{3}\)                      D. \(\dfrac{{7\pi }}{3}\)

Câu 18: Để phương trình \({\cos ^2}\left( {\dfrac{x}{2} - \dfrac{\pi }{4}} \right) = m\) có nghiệm ta chọn

A. \(m \le 1\)                            B. \(0 \le m \le 1\)

C. \( - 1 \le m \le 1\)                  D. \(m \ge 0\)

Câu 19: Phương trình \(\sin x + \cos x = 1 - \dfrac{1}{2}\sin 2x\) có nghiệm là:

A. \(x = \dfrac{\pi }{6} + k\dfrac{\pi }{2};\,\,x = k\dfrac{\pi }{4}\)

B. \(x = \dfrac{\pi }{8} + k\pi ;\,\,x = k\dfrac{\pi }{2}\)

C. \(x = \dfrac{\pi }{4} + k\pi ;\,\,x = k\pi \)

D. \(x = k2\pi ;\,\,x = \dfrac{\pi }{2} + k2\pi \)

Câu 20: Giải phương trình \(\dfrac{1}{{\sin 2x}} + \dfrac{1}{{\cos 2x}} = \dfrac{2}{{\sin 4x}}\)

A. \(x = \dfrac{\pi }{4} + k\pi ;\,\,x = k\pi \)

B. \(x = k\pi \)

C. Phương trình vô nghiệm

D. \(x = \dfrac{\pi }{4} + k\pi \)

II. PHẦN TỰ LUẬN

Câu 21: Giải các phương trình sau

\(a) \, 2\sin (x - {30^0}) - 1 = 0\)

\(b) \, 5{\sin ^2}x + 3\cos x + 3 = 0\)

Câu 22: Tìm GTLN, GTNN của hàm số \(y = 3 + \sin 2x\)