Chọn trục tọa độ Ox trùng với con đường H – P với O ≡ H, chiều dương là chiều từ H đến P.
a)
- Đường đi của xe:
+ Trên đoạn đường H – D: \(s{\rm{ }} = {\rm{ }}60t{\rm{ }}\left( {km,h} \right)\) với \(s{\rm{ }} \le {\rm{ }}60{\rm{ }}km\) và \(t{\rm{ }} \le {\rm{ }}1h\)
+ Trên đoạn đường D – P: \(s' = {\rm{ }}40\left( {t{\rm{ }}--{\rm{ }}2} \right){\rm{ }}\left( {km,h} \right)\) ; với \(t{\rm{ }} \ge {\rm{ }}2h\) .
- Phương trình chuyển động của xe:
+ Trên đoạn đường H – D: \(x{\rm{ }} = {\rm{ }}60t\) với \(x{\rm{ }} \le {\rm{ }}60{\rm{ }}km\) và\(t{\rm{ }} \le {\rm{ }}1h\).
+ Trên đoạn đường D – P: \(x' = {\rm{ }}60{\rm{ }} + {\rm{ }}40\left( {t{\rm{ }}--{\rm{ }}2} \right)\) với \(x' \ge {\rm{ }}60{\rm{ }}km\) và \(t{\rm{ }} \ge {\rm{ }}2{\rm{ }}h\) .
b) Đồ thị toạ độ - thời gian của xe trên cả quãng đường H - P:
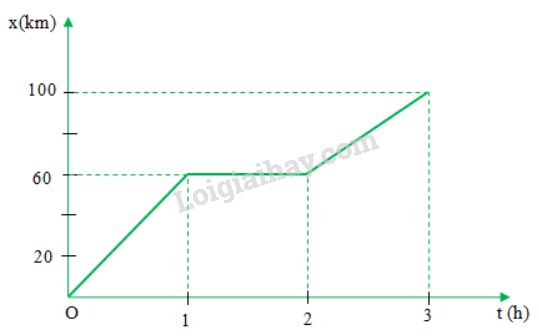
c) Dựa vào đồ thị ta thấy thời điểm xe đến P là 3 giờ.
d) Thời điểm xe đến P:
\({t_{HD}} + {t_{nghi}} + {t_{DP}}=\dfrac{{60}}{{60}} + 1 + \dfrac{{40}}{{40}} = 3(h)\)
Sau 3 giờ kể từ lúc xe xuất phát sẽ đến P.