Ta có \(A = F.S = 50.5 = 250J\)
Câu 24.6.
Một máy bay khối lượng 3000 kg khi cất cánh phải mất 80 s để bay lên tới độ cao 1500 m. Lấy g = 9,8 m/s2. Xác định công suất của động cơ máy bay. Cho rằng công mà động cơ máy bay sinh ra lúc này chủ yếu là để nâng máy bay lên cao.
Lực nâng máy bay lên cao phải có độ lớn bằng trọng lượng của máy bay :
F = P = mg = 3000.9,8 = 29400 N
Do đó, động cợ máy bay phải thực hiện công :
A = Fh = 29400.1500 ≈ 44.106 J
Suy ra công suất của động cơ máy bay : \(P = {A \over t} = {{{{44.10}^6}} \over {80}} = 550(kW)\)
Câu 24.7.
Một thang máy trọng lượng 10000 N có thể nâng được trọng lượng tối đa là 8000 N. Cho biết lực ma sát cản trở chuyển động của thang máy là 2000 N. Xác định công suất tối thiểu của động cơ thang máy để có thể nâng được trọng lượng tối đa lên cao với vận tốc không đổi là 2,0 m/s.
Do thang máy chuyển động đểu, nên lực kéo của động cơ thang máy phải có độ lớn :
F = P + Fms = (10000 + 8000) + 2000 = 20000 N
Suy ra động cơ thang máy phải có công suất tối thiểu : \(P = {A \over t} = {{Fs} \over t}\)
Thay v = s/t, ta tìm được : P = Fv = 20000.2,0 = 40 kW.
Câu 24.8.
Để kéo một vật khối lượng 80 kg lên xe ô tô tải, người ta dùng tấm ván dài 2,5 m, đặt nghiêng 30° so với mặt đất phẳng ngang, làm cầu nối với sàn xe. Biết lực kéo song song với mặt tấm ván và hệ số ma sát là 0,02. Lấy g ≈ 10 m/s2. Xác định công của lực kéo trong hai trường hợp :
a) Kéo vật chuyển động thẳng đều.
b) Kéo vật chuyển động thẳng với gia tốc 1,5 m/s2.
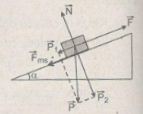
Chọn chiều chuyển động của vật m là chiều dương. Phương trình của định luật II Niu-tơn đối với vật m chuyển động trên mặt phẳng nghiêng như hình vẽ có dạng:
ma = F – P1 - Fms
Với P1 = mg.sin 300 ≈ 400 N.
Fms = µN = µmgcos 300 ≈ 13,8 N.
a. Khi vật chuyển động thẳng đều: a = 0, lực kéo có độ lớn:
F = P1 + Fms ≈ 413,8 N
Do đó, công của lực kéo: A = Fs = 413,8.2,5 = 1034,5 J.
b. Khi vật chuyển động với gia tốc a = 1,5 m/s2, lực kéo có độ lớn:
F = P1 + Fms+ ma ≈ 413,8 + 80.1,5 = 533,3 N
Công của lực kéo: A = Fs = 533,8.2,5 = 1334,5 J