Một người lái xuồng máy dự định mở máy cho xuôồng chạy ngang con sông rộng 240 m , mũi xuồng luôn luôn vuông góc với bờ sông . Nhưng do nước chảy nên xuồng sang đến bờ bên kia tại một địa điểm cách bến dự định 180 m về phía hạ lưu và xuồng đi hết 1 min. Xác định vận tốc của xuồng so với bờ sông.
Giải :
Coi xuồng là vật 1 ; Nước -2 ; Bờ -3
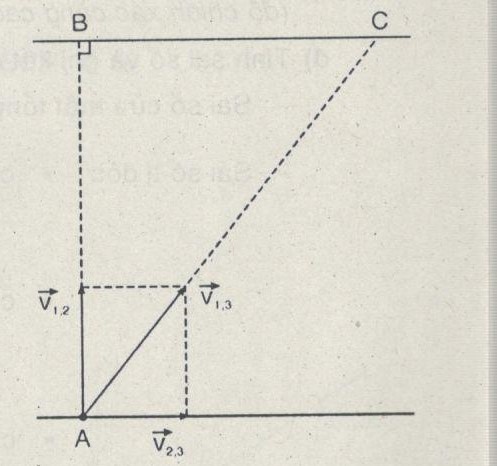
Có 2 cách giải sau
- Cách 1 : \(AC = \sqrt {A{B^2} + B{C^2}} = 300m\)
Vận tốc của xuồng so với bờ :
\({v_{13}} = {{AC} \over t} = {{300} \over {60}} = 5m/s\)
- Cách 2 :
\(\eqalign{ & {v_{23}} = {{BC} \over t} = {{180} \over {60}} = 3m/s \cr & {v_{12}} = {{AB} \over t} = {{240} \over {60}} = 4m/s \cr & {v_{13}} = \sqrt {v_{12}^2 + v_{23}^2} = 5m/s \cr} \)