Các lực tác dụng lên vật m được biểu diễn trên hình vẽ.
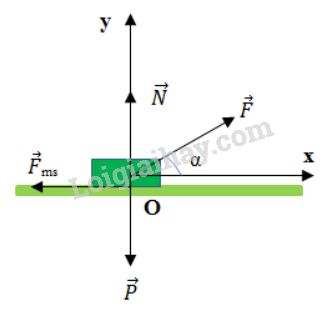
Áp dụng định luật II - Niuton: \(\vec F + \vec P + \vec N + \overrightarrow {{F_{m{\rm{s}}}}} = m\vec a\) (1)
Chọn hệ trục Oxy với chiều dương là chiều chuyển động theo phương Ox.
Chiếu phương trình (1) lên Ox ta được: \(Fcos\alpha - {F_{ms}} = ma\;\) (2)
Chiếu phương trình (1) lên Oy ta được: \(N + Fsin\alpha - P = 0 \Rightarrow N = P - Fsin\alpha \) (3)
Mà \({F_{ms}} = \;{\mu _t}N = {\mu _t}\left( {P - F\sin \alpha } \right)\) (4)
Từ (2), (3) và (4)
\(\eqalign{
& \Rightarrow Fcos\alpha - {\mu _t}(P - Fsin\alpha ) = ma \cr&\Rightarrow Fcos\alpha - {\mu _t}P + \mu Fsin\alpha = ma \cr
& \Rightarrow F(cosa + {\mu _t}sina) = ma + {\mu _t}mg \cr
& \Rightarrow F = {{m\left( {{\mu _t}g + a} \right)} \over {\cos \alpha + {\mu _t}.\sin \alpha }} \cr} \)
a) Khi a = 1,25 m/s2
\(F = {{4.\left( {0,3.10 + 1,25} \right)} \over {c{\rm{os}}30 + 0,3.\sin 30}} = {{4.\left( {0,3.10 + 1,25} \right)} \over {{{\sqrt 3 } \over 2} + 0,3.{1 \over 2}}} = 16,7N\)
b) Vật chuyển động thẳng đều a = 0.
\(F = {{4.\left( {0,3.10 + 0} \right)} \over {c{\rm{os}}30 + 0,3.\sin 30}} = {{4.\left( {0,3.10 + 0} \right)} \over {{{\sqrt 3 } \over 2} + 0,3.{1 \over 2}}} = 11,81N\).