Bài 22. Ngẫu lực

Chứng minh rằng momen của ngẫu lực không phụ thuộc vào vị trí của trục quay vuông góc với mặt phẳng chứa ngẫu lực.

Ngẫu lực là gì? Nêu một vài ví dụ về ngẫu lực.

Nêu tác dụng của ngẫu lực đối với một vật rắn?

Viết công thức tính momen của ngẫu lực. Momen của ngẫu lực có đặc điểm gì?

Hai lực của một ngẫu lực có độ lớn F = 5,0 N. Cánh tay đòn của ngẫu lực d = 20 cm. Momen của ngẫu lực là:

A. 100 N.m ;                                   B. 2,0 N.m ;

C. 0,5 N.m ;                                    D. 1,0 N.m.

Một ngẫu lực gồm có hai lực \(\overrightarrow{F_{1}}\) và \(\overrightarrow{F_{2}}\) có F₁ = F₂ = F và có cánh tay đòn d. Momen ngẫu lực này là:

A. (F₁ – F₂)d.

B. 2Fd

C. Fd

D. Chưa biết được vì còn phụ thuộc vào vị trí của trục quay.

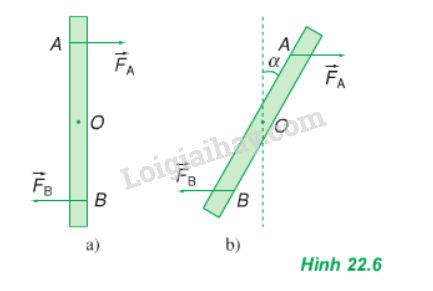
Một chiếc thước mảnh có trục quay nằm ngang đi qua trọng tâm O của thước. Dùng hai ngón tay tác dụng vào thước một ngẫu lực đặt vào hai điểm A và B cách nhau 4,5 cm và có độ lớn F_A = F_B = 1N (Hình 22.6a).

a) Tính momen của ngẫu lực.

b) Thanh quay đi một góc α = 30^o. Hai lực luôn luôn nằm ngang và vẫn đặt tại A và B (Hình 22.6b). Tính momen của ngẫu lực.