Các câu hỏi trắc nghiệm ôn tập chương III trang 122 SGK Hình học 11 Nâng cao

Câu 1 trang 122 SGK Hình học 11 Nâng cao

Cho tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây là sai ?

A. \(\overrightarrow {OG}  = {1 \over 4}\left( {\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD} } \right)\)

B. \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \)

C. \(\overrightarrow {AG}  = {2 \over 3}\left( {\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} } \right)\)

D. \(\overrightarrow {AG}  = {1 \over 4}\left( {\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} } \right)\)

Trả lời

(A), (B) đúng.

Gọi G₁ là trọng tâm ΔBCD ta có \(\overrightarrow {AG}  = {3 \over 4}\overrightarrow {A{G_1}}  = {1 \over 4}\left( {\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} } \right)\) nên (D) đúng.

Vậy chọn (C)

Câu 2 trang 122 SGK Hình học 11 Nâng cao

Mệnh đề nào sau đây là đúng ?

A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau ;

B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau ;

C. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia ;

D. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại.

Trả lời

Chọn (C)

Câu 3 trang 122 SGK Hình học 11 Nâng cao

Cho hai đường thẳng phân biệt a, b và mặt phẳng (P), trong đó a ⊥ (P). Mệnh đề nào sau đây là sai ?

A. Nếu b // (P) thì b ⊥ a

B. Nếu b ⊥ (P) thì b // a

C. Nếu b // a thì b ⊥ (P)

D. Nếu b ⊥ a thì b // (P)

Trả lời

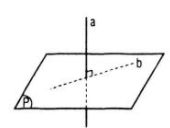
Nếu b ⊥ a thì có thể b ⊂ (P)

Chọn (D)

Câu 4 trang 122 SGK Hình học 11 Nâng cao

Tìm mệnh đề đúng trong các mệnh đề sau :

A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song ;

B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song ;

C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song ;

D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.

Trả lời

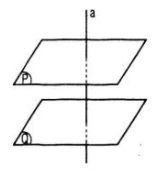
\(\left\{ {\matrix{   {(P) \ne (Q)}  \cr   {(P) \bot a}  \cr   {(Q) \bot a}  \cr } } \right. \Rightarrow (P)//(Q)\)

Chọn (C)

Câu 5 trang 122 SGK Hình học 11 Nâng cao

Mệnh đề nào sau đây là đúng ?

A. Hai đường thẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia ;

B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau ;

C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau ;

D. Ba mệnh đề trên đều sai.

Trả lời

Chọn D.

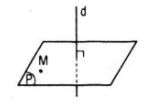
(A). Sai theo hình vẽ bên

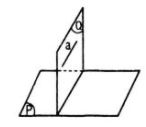
\(\left\{ {\matrix{   {(P) \bot (Q)}  \cr   {a \subset (Q)}  \cr } } \right.\) nhưng a // (P)

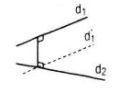
(B), (C) sai theo hình vẽ sau.

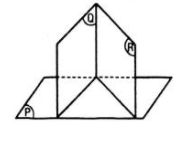
Câu 6 trang 123 SGK Hình học 11 Nâng cao

Trong các mệnh đề sau, mệnh đề nào đúng ?

A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước ;

B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước ;

C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước ;

D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Trả lời

Chọn (D)

Câu 7 trang 123 SGK Hình học 11 Nâng cao

Tìm mệnh đề đúng trong các mệnh đề sau :

A. Nếu hình hộp có hai mặt là hình chữ nhật thì nó là hình hộp chữ nhật ;

B. Nếu hình hộp có ba mặt là hình chữ nhật thì nó là hình hộp chữ nhật ;

C. Nếu hình hộp có bốn mặt là hình chữ nhật thì nó là hình hộp chữ nhật ;

D. Nếu hình hộp có năm mặt là hình chữ nhật thì nó là hình hộp chữ nhật.

Trả lời

Chọn (D)

Câu 8 trang 123 SGK Hình học 11 Nâng cao

Trong các mệnh đề sau, mệnh đề nào đúng ?

A. Nếu hình hộp có hai mặt là hình vuông thì nó là hình lập phương ;

B. Nếu hình hộp có ba mặt chung một đỉnh là hình vuông thì nó là hình lập phương ;

C. Nếu hình hộp có sáu mặt bằng nhau thì nó là hình lập phương ;

D. Nếu hình hộp có bốn đường chéo bằng nhau thì nó là hình lập phương .

Trả lời

Chọn (B)

Câu 9 trang 123 SGK Hình học 11 Nâng cao

Cho hình chóp S.ABC có đáy là tam giác đều. Tìm mệnh đề đúng trong các mệnh đề sau :

A. S.ABC là hình chóp đều nếu các mặt bên của nó là tam giác cân ;

B. S.ABC là hình chóp đều nếu các mặt bên của nó là tam giác cân với đỉnh S ;

C. S.ABC là hình chóp đều nếu góc giữa các mặt phẳng chứa các mặt bên và mặt phẳng chứa đáy bằng nhau ;

D. S.ABC là hình chóp đều nếu các mặt bên có diện tích bằng nhau.

Trả lời

Chọn (B)

Câu 10 trang 123 SGK Hình học 11 Nâng cao

Tìm mệnh đề đúng trong các mệnh đề sau :

A. Đường vuông góc chung của hai đường thẳng chéo nhau thì nằm trong mặt phẳng chứa đường thẳng này và vuông góc với đường thẳng kia ;

B. Đường vuông góc chung của hai đường thẳng chéo nhau thì vuông góc với mặt phẳng chứa đường thẳng này và song song với đường thẳng kia ;

C. Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó vuông góc với cả hai đường thẳng đó ;

D. Các mệnh đề trên đều sai.

Trả lời

Chọn (B)

Câu 11 trang 124 SGK Hình học 11 Nâng cao

Hình tứ diện ABCD có AB, AC, AD đôi một vuông góc là AB = AC = AD = 3.

Diện tích tam giác BCD bằng

A. \({{9\sqrt 3 } \over 2}\)

B. \({{9\sqrt 2 } \over 3}\)

C. 27

D. \({{27} \over 2}\)

Trả lời

Chọn (A).

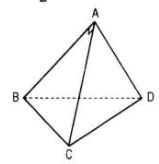
Ta có: BC = CD = BD = \(3\sqrt 2 \)

Tam giác BCD đều cạnh \(a = 3\sqrt 2 \) nên

\({S_{BCD}} = {{{a^2}\sqrt 3 } \over 4} = {{18\sqrt 3 } \over 4} = {{9\sqrt 3 } \over 2}\)

Câu 12 trang 124 SGK Hình học 11 Nâng cao

Hình hộp ABCD.A’B’C’D’ có AB = AA’ = AD = a và \(\widehat {A'AB} = \widehat {A'AD} = \widehat {BAD} = 60^\circ .\) Khi đó, khoảng cách giữa các đường thẳng chứa các cạnh đối diện của tứ diện AA’BD bằng :

A. \({{a\sqrt 2 } \over 2}\)

B. \({{a\sqrt 3 } \over 2}\)

C. \(a\sqrt 2 \)

D. \({{3a} \over 2}\)

Trả lời

Chọn (A)

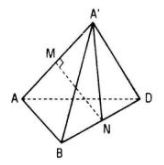
Tứ diện A’ABD là tứ diện đều cạnh a.

M, N lần lượt là trung điểm AA’, BD.

MN là đoạn vuông góc chung của AA’ và BD. Ta có:

\(M{N^2} = A'{N^2} - A'{M^2}\)

            \(= {\left( {{{a\sqrt 3 } \over 2}} \right)^2} - {\left( {{a \over 2}} \right)^2}\)

            \(= {{3{a^2}} \over 4} - {{{a^2}} \over 4} = {{{a^2}} \over 2} \)

\(\Rightarrow {\rm M}{\rm N} = {{a\sqrt 2 } \over 2}\)