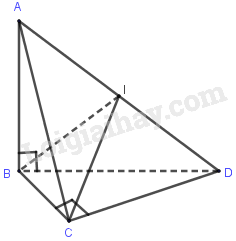
a. Ta có: CD ⊥ BC và CD ⊥ AB nên CD ⊥ (ABC)
mà AC ⊂ (ABC) do đó CD ⊥ AC.
Trong tam giác vuông ABC ta có:
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2}\)
Trong tam giác vuông ACD ta có:
\(A{D^2} = A{C^2} + C{D^2} = {a^2} + {b^2} + {c^2}\)
Suy ra: \(AD = \sqrt {{a^2} + {b^2} + {c^2}} \)
b. Ta có: \(AB \bot BC\) và \(AB \bot CD\) suy ra AB ⊥ (BCD) do đó AB ⊥ BD.
Gọi I là trung điểm AD ta có IC = IA = IB = ID.
Vậy I cách đều A, B, C, D.
c. Ta có: \(AB \bot \left( {BCD} \right)\) \( \Rightarrow BD\) là hình chiếu của \(AD\) trên \(\left( {BCD} \right)\).
Khi đó góc \(\widehat {\left( {AD,\left( {BCD} \right)} \right)} = \widehat {\left( {AD,BD} \right)} = \widehat {ADB}\).
Xét tam giác \(ABD\) vuông tại \(B\) thì \(\sin \widehat {ADB} = \dfrac{{AB}}{{AD}} = \dfrac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\) \( \Rightarrow \widehat {\left( {AD,\left( {BCD} \right)} \right)} = \arcsin \dfrac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
Lại có \(DC \bot \left( {ABC} \right)\) \( \Rightarrow AC\) là hình chiếu của \(AD\) trên \(\left( {ABC} \right)\).
Khi đó góc \(\widehat {\left( {AD,\left( {ABC} \right)} \right)} = \widehat {\left( {AD,AC} \right)} = \widehat {DAC}\)
Xét tam giác \(ACD\) vuông tại \(C\) thì \(\sin \widehat {DAC} = \dfrac{{CD}}{{AD}} = \dfrac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\) \( \Rightarrow \widehat {\left( {AD,\left( {ABC} \right)} \right)} = \arcsin \dfrac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)