a. Đặt a = OA, b = OB, c = OC. Ta có:
\(AB = \sqrt {{a^2} + {b^2}} ,BC = \sqrt {{b^2} + {c^2}} ,AC = \sqrt {{a^2} + {c^2}} \)
Áp dụng định lí cosin trong tam giác ABC ta có :
\(\cos A = {{A{B^2} + A{C^2} - B{C^2}} \over {AB.AC}} = {{{a^2} + {b^2} + {a^2} + {c^2} - {b^2} - {c^2}} \over {AB.AC}} = {{2{a^2}} \over {AB.AC}} > 0\)
⇒ A nhọn. Tương tự B, C là các góc nhọn.
Vậy ΔABC có ba góc nhọn.
b.
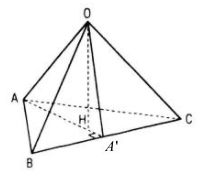
Vì H là hình chiếu của điểm O trên mp(ABC)
nên OH ⊥ (ABC)
Mặt khác OA ⊥ (OBC) nên OA ⊥ BC.
Vậy AH ⊥ BC (định lí ba đường vuông góc), tức
là H thuộc một đường cao của tam giác ABC
Tương tự như trên ta cũng có H thuộc đường cao
thứ hai của tam giác ABC.
Vậy H là trực tâm tam giác ABC
c. Nếu AH ⊥ BC tại A’ thì BC ⊥ OA’.
Vì OH là đường cao của tam giác vuông AOA’ (vuông tại O) và OA’ là đường cao của tam giác vuông BOC (vuông tại O) nên :
\({1 \over {O{H^2}}} = {1 \over {O{A^2}}} + {1 \over {OA{'^2}}},{1 \over {OA{'^2}}} = {1 \over {O{B^2}}} + {1 \over {O{C^2}}}\)
Vậy \({1 \over {O{H^2}}} = {1 \over {O{A^2}}} + {1 \over {O{B^2}}} + {1 \over {O{C^2}}}\)