Giải
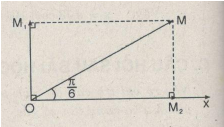
Chọn gốc thời gian sao cho pha ban đầu của dao động thứ hai bằng \(0\) thì dao động thứ nhất sẽ sớm pha hơn dao động thứ hai một góc \({\pi \over 2}\).
Suy ra :\({x_1} = 100\cos \left( {50t + {\pi \over 2}} \right)(mm);{x_2} = 173\cos 50t(mm)\)
Ta có thể giải bằng phương pháp vectơ quay.
\(\eqalign{
& OM = \sqrt {OM_1^2 + OM_2^2} \cr
& = \sqrt {{{100}^2} + {{173}^2}} \approx 200(mm) \cr
& \tan \varphi = {{O{M_1}} \over {O{M_2}}} = {{100} \over {173}} =0,578 \Rightarrow \varphi = {\pi \over 6} \cr} \)
Vậy \(x = 200\cos \left( {50t + {\pi \over 6}} \right)(mm)\)
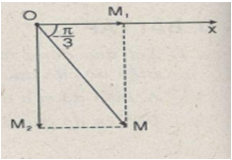
Cách khác : Ta có thể cho dao động thứ hai trễ pha \({\pi \over 2}\) so với dao động thứ nhất 1 góc \({\pi \over 2}\) thì :
\(\eqalign{
& {x_1} = 100\cos 50t(mm);{x_2} = 173\cos \left( {50t - {\pi \over 2}} \right)(mm) \cr
& OM = \sqrt {OM_1^2 + OM_2^2} = 200(mm) \cr} \)
Và \(\tan \varphi = - {{O{M_2}} \over {O{M_1}}} = - 1,73\Rightarrow \varphi = - {\pi \over 3}.\)
Vậy : \(x = 200\cos \left( {50t - {\pi \over 3}} \right)(mm)\)