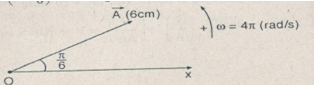
Giải
Phương trình dao động của vật :\(x = 6\cos \left( {4\pi t + {\pi \over 6}} \right)(cm)\)
a) Biên độ \(A =6\) (cm)
Chu kì \(T = {{2\pi } \over \omega } = {{2\pi } \over {4\pi }} = 0,5(s)\)
Tần só góc \(\omega = 4\pi (rad/s)\)
Tần số \(f = {1 \over T} = {1 \over {0,5}} = 2(Hz)\)
b) Khi \(t = {1 \over 4}(s) \Rightarrow pha\;(\omega t + \varphi ) = \left( {4\pi .{1 \over 4} + {\pi \over 6}} \right) = {{7\pi } \over 6}\)
\( \Rightarrow x = 6\cos \left( {\pi + {\pi \over 6}} \right) = - 6\cos {\pi \over 6} = - 6.{{\sqrt 3 } \over 2} = - 3\sqrt 3 (cm).\)
c) Vẽ vectơ quay biểu diễn dao động vào thời điểm \(t =0\):