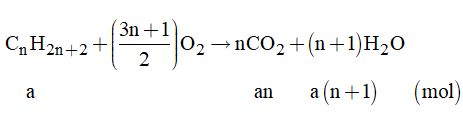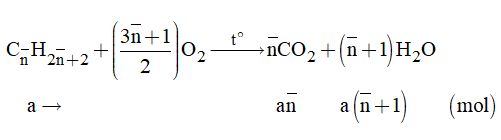Đề kiểm tra 15 phút - Đề số 1 - Chương V - Hóa học 11
Lời giải
Bài Tập và lời giải
Câu 2 trang 41 SGK Công Nghệ 7
Xử lí hạt giống nhằm mục đính gì ? Ở địa phương em có tiến hành xử lí hạt giống không , nếu có thì thường xử lí theo cách nào ?
Câu 3 trang 41 SGK Công Nghệ 7
Em hãy nêu Ưu, nhược điểm của các phương pháp gieo trồng ?