Đề số 16 - Đề kiểm tra học kì 1 - Toán 7

Đề bài

Phần I: Trắc nghiệm

            Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm.

Câu 1 :Kết quả của phép tính \(\dfrac{{ - 8}}{{15}}:\left( {\dfrac{{ - 4}}{5}} \right)\) là

A.\(\dfrac{{ - 2}}{3}\) .                       B.\(\dfrac{{ - 3}}{2}\).

C.\(\dfrac{2}{3}\).                              D.\(\dfrac{3}{2}\).\(\)

Câu 2 :Viết biểu thức (1,5)³.8 dưới dạng một lũy thừa được kết quả là

A.12³                            B. (1,5)²⁴

C. (12)²⁴                      D. 3³

Câu 3 :Nếu \(\sqrt x  = 9\) thì x có giá trị bằng

A. 3.                            B. 9.

C. 18.                          D. 81.

Câu 4 : Khẳng định nào sau đây không đúng?

A.\(\left| { - 0,5} \right| = 0,5\)            B.\(\left| { - 0,5} \right| =  - 0,5\)

C.\(\left| { - 0,5} \right| = \left| {0,5} \right|\)  D.\(\left| { - 0,5} \right| =  - ( - 0,5).\)

Câu 5 : Cho x và y là hai đại lượng tỉ lệ thuận và khi x = 6 thì y = 4. Hệ số tỉ lệ k của y đối với x là:

A.\(\dfrac{2}{3}\).                              B. .

C.\(\dfrac{1}{{24}}\)  .                       D.\(24\).

Câu 6 : Cho hai đường thẳng a và b song song với nhau. Nếu đường thẳng c vuông góc với đường thẳng a thì hai đường thẳng c và b

A. song song với nhau

B. vuông góc với nhau

C. trùng nhau 

D. không cắt nhau

Câu 7 : Cho \(\Delta ABC\) vuông ở A, \(\angle ABC = {60^0}\). Tia phân giác của ACB cắt AB tại M. Số đo của góc AMC bằng

A. 15⁰                          B. 30⁰

C. 60⁰                          D. 75⁰.

Câu 8 : Cho \(\Delta ABC = \Delta MNE\). Biết \(A = {30^0}\); \(N = {65^0}\). Số đo của góc C bằng

A. 30⁰                          B. 65⁰

C. 85⁰                          D. 95⁰.

Phần II. Tự luận 

Câu 1 : 

1) Thực hiện phép tính:          

a) \(\left( { - 3} \right) - \left( { - \dfrac{3}{4}} \right)\).       

b) \(2:{\left( {\dfrac{1}{2} - \dfrac{2}{3}} \right)^2} - \sqrt {{3^2} + {4^2}} \).

2) Tìm x, biết: \(\dfrac{2}{{3.5}} = \dfrac{{\left| {x - 1} \right|}}{7}\).

Câu 2 : Trong đợt vận động ủng hộ đồng bào miền Trung bị lũ lụt. Học sinh ba lớp 7A, 7B, 7C ở một trường THCS đã ủng hộ được 36 thùng sách, vở các loại. Biết số thùng sách, vở mà mỗi lớp 7A, 7B, 7C ủng hộ lần lượt tỉ lệ với 2; 3; 4. Tính số thùng sách, vở mỗi lớp đã ủng hộ.

Câu 3 : Cho tam giác ABC vuông tại A, có AB = AC. Gọi H là trung điểm của cạnh BC.

1) Chứng minh \(\Delta AHB = \Delta AHC\).

2) Chứng minh AH vuông góc với BC.

3) Trên tia đối của tia AH lấy điểm E sao cho AE = BC, trên tia đối của tia CA lấy điểm F sao cho CF = AB. Tính số đo của góc EBF.

Câu 4 :  Cho ba số a, b, c dương. Chứng tỏ rằng \(M = \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}}\) không là số nguyên.\(\)

Phần I: Trắc nghiệm

Phần II. Tự luận

Câu 1:

1) Thực hiện phép tính:

\(\begin{array}{l}a)\;\;( - 3) - \left( { - \dfrac{3}{4}} \right) \\= \left( { - \dfrac{{3.4}}{4}} \right) - \left( { - \dfrac{3}{4}} \right) \\= \dfrac{{ - 12 + 3}}{4} = \dfrac{{ - 9}}{4}\\b)\;\;2:{\left( {\dfrac{1}{2} - \dfrac{2}{3}} \right)^2} - \sqrt {{3^2} + {4^2}}\\  \;\;\;= 2:{\left( {\dfrac{{1.3}}{{2.3}} - \dfrac{{2.2}}{{3.2}}} \right)^2} - \sqrt {9 + 16} \\\;\;\; = 2:{\left( {\dfrac{{3 - 4}}{6}} \right)^2} - \sqrt {25} \\\;\;\; = 2:{\left( {\dfrac{{ - 1}}{6}} \right)^2} - \sqrt {{5^2}} \\\;\;\; = 2:\dfrac{1}{{36}} - 5 = 2.36 - 5 = 67.\end{array}\)

2) Tìm \(x,\) biết \(\dfrac{2}{{3.5}} = \dfrac{{\left| {x - 1} \right|}}{7}.\)

\(\begin{array}{l}\;\;\;\;\dfrac{2}{{3.5}} = \dfrac{{\left| {x - 1} \right|}}{7} \Leftrightarrow \left| {x - 1} \right| = \dfrac{{2.7}}{{3.5}} = \dfrac{{14}}{{15}}\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = \dfrac{{14}}{{15}}\\x - 1 =  - \dfrac{{14}}{{15}}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{14}}{{15}} + 1 = \dfrac{{29}}{{15}}\\x =  - \dfrac{{14}}{{15}} + 1 = \dfrac{1}{{15}}\end{array} \right..\end{array}\)

Vậy x = \(\dfrac{{29}}{{15}}\), x = \(\dfrac{1}{{15}}\)

Câu 2:

Gọi số thùng sách, vở mà mỗi lớp 7A, 7B, 7C ủng hộ lần lượt là \(x,\;y,\;z\;\;\;\left( {x,\;y,\;z \in N*} \right)\) (thùng).

Tổng số thùng sách 3 lớp ủng hộ là:\(x + y + z = 36.\)

Biết số thùng sách, vở mà mỗi lớp 7A, 7B, 7C ủng hộ lần lượt tỉ lệ với 2; 3; 4.

Suy ra:\(\)\(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{4}\)

Theo tính chất dãy tỉ số bằng nhau ta có:

            \(\begin{array}{l}\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{4} = \dfrac{{x + y + z}}{{2 + 3 + 4}} = \dfrac{{36}}{9} = 4\\ \Rightarrow \left\{ \begin{array}{l}x = 2.4 = 8\;\;\left( {tm} \right)\\y = 3.4 = 12\;\;\left( {tm} \right)\\z = 4.4 = 16\;\;\left( {tm} \right)\end{array} \right..\end{array}\)

Vậy lớp 7A, 7B, 7C ủng hộ số thùng sách, vở lần lượt là 8, 12 và 16 thùng.

Câu 3:

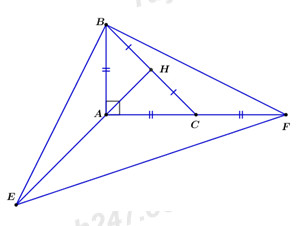
1) Theo đề bài ta có: \(\Delta ABC\) vuông tại A và AB = AC.

\( \Rightarrow \Delta ABC\) vuông cân tại A.

\( \Rightarrow \angle ABH = \angle ACH = {45^0}\) (2 góc đáy bằng nhau) \(\)

Xét \(\Delta AHB\) và \(\Delta AHC\) ta có:

BH = HC (H là trung điểm của BC)

AB = AC (theo giả thiết)

\(\angle ABH = \angle ACH\) (chứng minh trên)

\( \Rightarrow \Delta AHB = \Delta AHC\;(c - g - c)\) (đpcm)

\( \Rightarrow \angle BAH = \angle CAH\) (hai góc tương ứng)

2) Mà \(\angle BAC = \angle BAH + \angle HAC = {90^0} \)

\(\Rightarrow \angle BAH = \angle CAH = \dfrac{1}{2}\angle BAC = {45^0}\)

Xét tam giác AHB, ta có:

\(\begin{array}{l}\angle ABH + \angle BAH + \angle AHB = {180^0}\\ \Leftrightarrow {45^0} + {45^0} + \angle AHB = {180^0}\\ \Leftrightarrow \angle AHB = {90^0}\end{array}\)

\( \Rightarrow AH \bot BC\) (đpcm) \(\Delta AMB\)

3) Ta có: \(\angle E{\rm{A}}H = \angle E{\rm{A}}B + \angle BAH = {180^0}\) (góc bẹt)

\(\begin{array}{l} \Rightarrow \angle E{\rm{A}}B + {45^0} = {180^0}\\ \Leftrightarrow \angle E{\rm{A}}B = {180^0} - {45^0} = {135^0}\end{array}\)

Ta lại có: \(\angle ACF = \angle ACB + \angle BCF = {180^0}\) (góc bẹt)

\(\begin{array}{l} \Rightarrow \angle BCF + {45^0} = {180^0}\\ \Leftrightarrow \angle BCF = {180^0} - {45^0} = {135^0}\end{array}\)

 Xét tam giác EAB và tam giác BCF có:

                        AE = CB (giả thiết)

                        CF = AB (giả thiết)

                        \(\angle BCF = \angle E{\rm{A}}B = {135^0}\) (chứng minh trên)

\( \Rightarrow \Delta E{\rm{A}}B = \Delta BCF\;(c - g - c)\)

\( \Rightarrow \angle CFB = \angle ABE\) (hai góc tương ứng bằng nhau)

\( \Rightarrow \angle FBC + \angle ABE = \angle FBC + \angle CFB = \angle ACB = {45^0}\)(góc ngoài của tam giác)

Vậy: \(\angle EBF = \angle EBA + \angle ABC + \angle CBF = {45^0} + {45^0} = {90^0}\)

Câu 4:

Ta có:

\(\begin{array}{l}\dfrac{a}{{a + b}} > \dfrac{a}{{a + b + c}}\\\dfrac{b}{{b + c}} > \dfrac{b}{{a + b + c}}\\\dfrac{c}{{c + a}} > \dfrac{c}{{a + b + c}}\end{array}\)

Cộng vế với vế ta được:

\(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} > \dfrac{a}{{a + b + c}} + \dfrac{b}{{a + b + c}} + \dfrac{c}{{a + b + c}}\)\(\,\left( { = \dfrac{{a + b + c}}{{a + b + c}} = 1} \right)\)         (1)

Lại có:

\(\begin{array}{l}\dfrac{a}{{a + b}} < \dfrac{{a + c}}{{a + b + c}}\\\dfrac{b}{{b + c}} < \dfrac{{b + a}}{{a + b + c}}\\\dfrac{c}{{c + a}} < \dfrac{{c + b}}{{a + b + c}}\end{array}\)

Cộng vế với vế ta được:

\(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} < \dfrac{{a + c}}{{a + b + c}} + \dfrac{{b + a}}{{a + b + c}} + \dfrac{{c + b}}{{a + b + c}}\)\(\,\left( { = \dfrac{{2(a + b + c)}}{{a + b + c}} = 2} \right)\)                (2)

Từ (1) và (2) ta có: \(1 < \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} < 2\)

\( \Rightarrow \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}}\) không phải là số nguyên (đpcm).