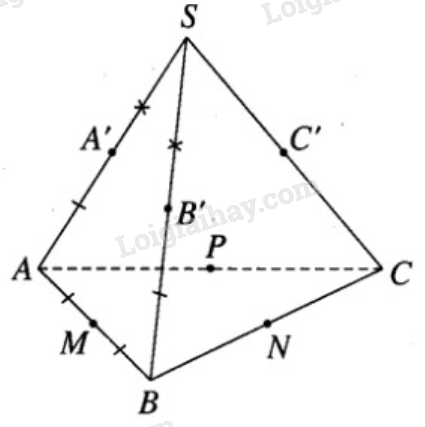
Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và A’ , B’, C’ là các điểm tiếp xúc của các cạnh bên SA, SB, SC với mặt cầu. Ta có AA’ và AM là hai tiếp tuyến nên AM = AA’. Vì M là trung điểm của AB nên AM = MB.
Mặt khác BM = BB’, ta suy ra AA’ = BB’
Vì SA’ = SB’ nên SA’ + A’A = SB’ + B’B hay SA = SB.
Tương tự, ta chứng minh được SB = SC
Do đó SA = SB = SC.
Mặt khác AB = 2BM = 2BN = BC = 2CN=2CP = CA
Vậy AB = BC = CA và ABC là một tam giác đều nên là một hình chóp đều. Ta có đường cao kẻ từ S có chân H là tâm đường tròn ngoại tiếp tam giác đều ABC.