Thứ tự các vật tư trái sang phải là 1 - 2 - 3 Gia tốc của hệ vật: \(a = \dfrac{F}{{3m}}\)Xét riêng từng vật:+ Với vật 1, lực tác dụng lên nó là lực căng \({T_1}\)\({T_1} = {m_1}a = m.\dfrac{F}{{3m}} = \dfrac{F}{3}\)+ Với vật 3, lực tác dụng lên nó bao gồm lực F và lực căng \({T_2}\)\(F - {T_2} = {m_2}a = m.\dfrac{F}{{3m}} = \dfrac{F}{3} \\\to {T_2} = F - \dfrac{F}{3} = \dfrac{{2F}}{3}\)+ Hợp lực tác dụng lên vật 2.\({T_2} - {T_1} = \dfrac{{2F}}{3} - \dfrac{F}{3} = \dfrac{F}{3}\)
Chọn đáp án D
III.2.
Một hình lập phương tiết diện ABCD, có trọng lượng 50N đặt trên mặt bàn nằm ngang (H.III.2). Phải tác dụng vào hình này một lực đẩy có phương song song với AD và có độ lớn tối thiểu bằng bao nhiêu để hình quay quanh D còn A bênh lên khỏi mặt bàn?
A. 50 N
B. 25 N
C. 12,5 N
D. 2,5 N
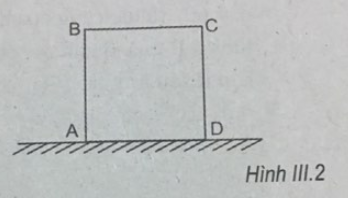
Chọn đáp án B
III.3.
Một thanh đồng chất, dài L, trọng lượng P tựa vào tường không ma sát. Mặt sàn nhám và có hệ số ma sát trượt là µ. Thang đang đứng yên ở vị trí có góc nghiêng so với sàn là α (H.III.2). Khi giảm góc nghiêng α xuống đến quá giá trị α1 thì thang bắt đầu trượt. Coi một cách gần đúng lực ma sát nghỉ cực đại bằng lực ma sát trượt. Góc α1 là
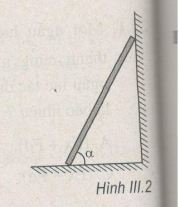
A. tan α1= 2µ.
B. \(\tan {\alpha _1} = \displaystyle{1 \over {2\mu }}\)
C. cos α1 = µ.
D. sin α1 = µ.
Gọi \(\overrightarrow Q \)là phản lực của tường tác dụng lên thanh tại đầu B. Gọi \(\overrightarrow R \)là phản lực của sàn nhà tác dụng lên thanh tại đầu A. Phản lực \(\overrightarrow R \)gồm phản lực pháp tuyến \(\overrightarrow N \)và phản lực tiếp tuyến \(\overrightarrow {{F_{msn}}} \) (hình vẽ). Ta trượt các vecto trên giá của chúng đến điểm đồng quy O. Ta có:
\(\overrightarrow P + \overrightarrow Q + \overrightarrow R = \overrightarrow 0 \)hay \(\overrightarrow Q + \overrightarrow R = - \overrightarrow P \)
Từ hình vẽ ta có:
\(\tan \theta = \dfrac{{{F_{msn}}}}{N} = \mu \)
\(\tan \theta = \dfrac{{AH}}{{OH}} = \dfrac{{L\cos {\alpha _1}}}{{2.L\sin {\alpha _1}}} = \dfrac{1}{{2\tan {\alpha _1}}}\)
Suy ra \(\tan {\alpha _1} = \dfrac{1}{{2\mu }}\)
Chọn đáp án B