a. Ta có: \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \)
và \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} \)
Vậy \(\overrightarrow {AC'} .\overrightarrow {BD} = \left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right).\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right) = 0\)
Tương tự, ta có: \(\overrightarrow {AC'} .\overrightarrow {BA'} = 0\)
Vậy AC’ ⊥ (A’BD)
Do (A’BD) // (B’CD’) nên AC’ ⊥ (B’CD’)
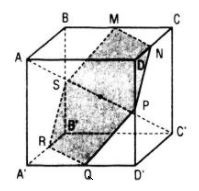
b. Gọi M là trung điểm của BC thì MA = MC’ (vì cùng bằng \({{a\sqrt 5 } \over 2}\) ) nên M thuộc mặt phẳng trung trực (α) của AC’
Tương tự, ta chứng minh được N, P, Q, R, S cũng có tính chất đó (N, P, Q, R, S lần lượt là trung điểm của CD, DD’, D’A’, A’B’, B’B).
Vậy thiết diện của hình lập phương bị cắt bởi mp(α) là MNPQRS. Đây là lục giác đều cạnh bằng \({{a\sqrt 2 } \over 2}\). Từ đó ta tính được diện tích của thiết diện là : \(S = 6.{\left( {{{a\sqrt 2 } \over 2}} \right)^2}.{{\sqrt 3 } \over 4} = {{3\sqrt 3 } \over 4}{a^2}.\)