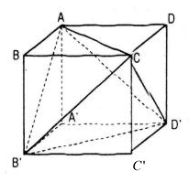
a. Ta có: B’D’ = BD
Vậy AC = B’D’ ⇔ AC = BD, khi đó ABCD là hình chữ nhật
Tương tự ta cũng có ABB’A’ và ADD’A’ là những hình chữ nhật. Vậy khi tứ diện AB’CD’ có các cạnh đối diện bằng nhau thì ABCD.A’B’C’D’ là hình hộp chữ nhật.
Ngược lại, khi ABCD.A’B’C’D’ là hình hộp chữ nhật thì dễ thấy tứ diện AB’CD’ có các cạnh đối diện bằng nhau.
b. Ta có: BD // B’D’. Vậy AC ⊥ B’D’ ⇔ AC ⊥ BD. Khi đó ABCD là hình thoi. Tương tự như trên ta cũng có ABB’A’ và ADD’A’ là những hình thoi. Vậy hình hộp ABCD.A’B’C’D’ là hình hộp thoi (tức sáu mặt của hình hộp là hình thoi).
Cũng dễ thấy rằng nếu ABCD.A’B’C’D’ là hình hộp thoi thì tứ diện AB’CD’ có các cạnh đối diện vuông góc.
c. Khi AB’CD’ là tứ diện đều thì các cạnh đối diện vừa bằng nhau vừa vuông góc; áp dụng kết quả của các câu a và b ta có : Khi AB’CD’ là tứ diện đều thì hình hộp ABCD.A’B’C’D’ là hình lập phương.
Ngược lại, nếu ABCD.A’B’C’D’ là hình lập phương thì AB’CD’ là tứ diện đều.