Giả sử M(x0, lnx0) ∈ (C) (x0 > 0 )
Ta có: \(y' = {1 \over x}\)
Tiếp tuyến của (C) tại M có phương trình là:
\(y = {1 \over {{x_0}}}(x - {x_o}) + \ln {x_0}\)
Vậy với mọi x ∈ (0,+∞), ta cần chứng minh:
\(\eqalign{
& {1 \over {{x_0}}}(x - {x_0}) + \ln {x_0} \ge \ln x \cr
& \Leftrightarrow {x \over {{x_0}}} - 1 - \ln {x \over {{x_0}}} \ge 0 \cr} \)
Đặt \(t = {x \over {{x_0}}} > 0\)
Xét hàm số \(g(t) = t – \ln t\) với t > 0
\(\eqalign{
& g' = 1 - {1 \over t} = {{t - 1} \over t} \cr
& g' = 0 \Leftrightarrow y = t = 1 \cr} \)
Bảng biến thiên
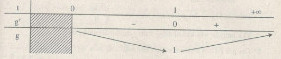
Từ bảng biến thiên ta có \(g(t) ≥ 1\) với mọi \(t \in (0, +∞)\)
\( \Rightarrow t - \ln t - 1 \ge 0 \Rightarrow {x \over {{x_0}}} - 1 - \ln {x \over {{x_0}}} \ge 0\) với mọi \(x > 0\)
Vậy trên \((0; +∞)\) (C) nằm phía dưới đường thẳng (D)