Đề số 3 – Đề kiểm tra học kì 2 – Toán 8

I. Trắc nghiệm: 

Đọc kĩ các câu hỏi và chọn đáp án đúng của các câu trả lời đã cho ở bên dưới. Ví dụ: Câu 1 chọn đáp án A thì ghi là: 1A…

Câu 1. Cho \(\left| a \right|\, = \,5\)thì:

A. a = 5.

B. a = - 5.

C. a = \( \pm \)5.

D. Một đáp án khác.

Câu 2. Hình hộp chữ nhật là hình có bao nhiêu mặt ?

A. 6 mặt.

B. 5 mặt.

C. 4 mặt.

D. 7 mặt.

Câu 3. Điều kiện xác định của phương trình \(\dfrac{x}{{x + 3}} - \dfrac{{x - 1}}{x} = 1\) là:

A. x\( \ne \)0.

B. x\( \ne \)3.

C.  x\( \ne \)0 và x\( \ne \)3.

D. x\( \ne \)0 và x\( \ne \)-3.         

Câu 4. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn ?

A. x + y > 2.

B.  0.x – 1 \( \ge \) 0.

C.   2x –5 >  1.           

D. (x – 1)² \( \le \) 2x.

Câu 5. Nghiệm của bất phương trình 6 – 3x < 15 là:

A.  x >– 5.

B. x <– 5.

C.  x < –3.

D.  x > –3.

Câu 6. Hình sau biểu diễn tập nghiệm của bất phương trình nào?

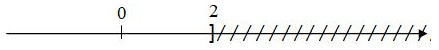
A. x ≤ 2.

B. x > 2.

C. x ≥ 2.

D. x <2. 

Câu 7. Trong các phương trình sau, phương trình nào không có một nghiệm duy nhất ? 

A. 8 + x = 4.

B. 2 – x = x – 4.

C. 1 + x =  x.

D. 5 + 2x = 0.

Câu 8. Nếu tam giác ABC có MN//BC, \((M \in AB,N \in AC)\) theo định lý Talet ta có:

A.  \(\dfrac{{AM}}{{MB}} = \dfrac{{AN}}{{NC}}\).

B. \(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{NC}}\).

C. \(\dfrac{{AM}}{{MB}} = \dfrac{{AN}}{{AC}}\).

D.\(\dfrac{{AB}}{{MB}} = \dfrac{{AN}}{{NC}}\).

Câu 9.  Phương trình nào sau đây là phương trình bậc nhất một ẩn ?

A. 0x + 2 = 0.

B.\(\dfrac{x}{{{x^2} + 1}}.\)

C. x + y = 0.

D. 2x + 1 = 0.

Câu 10.  Nếu \(\Delta\) MNP đồng dạng \(\Delta\) DEF thì ta có tỉ lệ thức nào đúng nhất ?

A. \(\dfrac{{MN}}{{DE}} = \dfrac{{MP}}{{DF}}\).

B. \(\dfrac{{MN}}{{DE}} = \dfrac{{NP}}{{EF}}\).

C.  \(\dfrac{{NP}}{{DE}} = \dfrac{{{\rm{EF}}}}{{MN}}\).

D. \(\dfrac{{MN}}{{DF}} = \dfrac{{NP}}{{{\rm{EF}}}} = \dfrac{{MP}}{{DE}}\).

Câu 11. Dựa vào hình vẽ trên cho biết, x =  ?                              

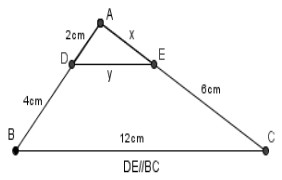
A. 9cm.

B. 6cm.

C. 1cm.

D. 3cm.

Câu 12. Tập nghiệm của phương trình x – 1 = 0 là:

A. {0} .

B. {1}.

C. {1;0}.

D. {–1}.                       

II. Tự luận:

Câu 1. 

a) Giải phương trình: (3x – 2)(4x + 5) = 0.

b) Giải bất phương trình sau và biểu diễn tập hợp nghiệm trên trục số: \(\dfrac{{2x - 3}}{2} > \dfrac{{8x - 11}}{6}.\)

Câu 2. 

Học kì I, số học sinh giỏi của lớp 8 A bằng \(\dfrac{1}{8}\) số học sinh cả lớp. Sang học kì II, có thêm 3 bạn phấn đấu trở thành học sinh giỏi nữa, do đó số học sinh giỏi bằng 20% số học sinh cả lớp. Hỏi lớp 8A có bao nhiêu học sinh ?

Câu 3.

Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A \(({\rm{D}} \in {\rm{BC}}\)).

a. Tính \(\dfrac{{{\rm{DB}}}}{{{\rm{DC}}}}\) .

b. Kẻ đường cao AH (\({\rm{H}} \in {\rm{BC}}\)). Chứng minh rằng: \({\rm{\Delta AHB}}\) đồng dạng \({\rm{\Delta CHA}}\).

c.Tính: \(\dfrac{{{S_{\Delta AHB}}}}{{{S_{\Delta CHA}}}}.\)

I. Trắc nghiệm: : Mỗi câu  đúng được

II. Tự luận: 

Câu 1:

a) \((3x – 2)(4x + 5) = 0.\)

\( \Leftrightarrow 3x – 2 = 0\) hoặc  \(4x + 5 = 0.\)

 \( \Leftrightarrow  x = \dfrac{2}{3}\)  hoặc \(x = - \dfrac{5}{4}\).

Vậy: nghiệm của phương trình là: \(x = \dfrac{2}{3}\); \(x = - \dfrac{5}{4}\).

b) \(\dfrac{{2x - 3}}{2} > \dfrac{{8x - 11}}{6}.\)

\( \Leftrightarrow  6x – 9 > 8x – 11\)

\( \Leftrightarrow  2x < 2\)

\( \Leftrightarrow x < 1\)

Vậy: \(S = \left\{ {x\;\left| {\,x < 1} \right.} \right\}\)

Biểu diễn trên trục số

Câu 2: Gọi x là số học sinh cả lớp ( điều kiện là x nguyên dương).

Số học sinh giỏi của kớp 8A ở học kì I là: \(\dfrac{x}{8}\).

Số học sinh giỏi lớp 8A ở học kì II là: \(\dfrac{x}{8}+ 3.\)

Theo đề ta có pt: \(\dfrac{x}{8}+ 3 = \dfrac{{20}}{{100}}x\).

Giải pt, ta được: \(x = 40.\)

Vậy: số học sinh lớp 8A là 40 ( học sinh).

Câu 3:

Vẽ hình đúng.

a) Ta có: AD là phân giác góc A của tam giác ABC

     Nên: \(\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}} = \dfrac{6}{8} = \dfrac{3}{4}.\)

b) Xét \(\Delta\) AHB và \(\Delta\) CHA, có:

\(\widehat {{H_2}} = \widehat {{H_1}}\)= 90⁰.

 \(\widehat B = \widehat {HAC}\)(cùng phụ với \(\widehat {HAB}\)).

Suy ra: \(\Delta\) AHB  đồng dạng  \(\Delta\) CHA (g-g).

c) Ta có: \(\Delta\) AHB  đồng dạng  \(\Delta\) CHA.

Nên:\(\dfrac{{{\rm{AH}}}}{{{\rm{CH}}}}{\rm{ = }}\dfrac{{HB}}{{HA}} = \dfrac{{AB}}{{{\rm{AC}}}} = k\)    

Suy ra: \(k\,{\rm{ = }}\dfrac{{AB}}{{AC}} = \dfrac{{\rm{4}}}{3}\)                            

Mà: \(\dfrac{{{{\rm{S}}_{\Delta {\rm{AHB}}}}}}{{{{\rm{S}}_{\Delta {\rm{CHA}}}}}} = {k^2}.\)

Vậy: \(\dfrac{{{{\rm{S}}_{\Delta {\rm{AHB}}}}}}{{{{\rm{S}}_{\Delta {\rm{CHA}}}}}} = {\left( {\dfrac{4}{3}} \right)^2} = \dfrac{{16}}{9}.\)