Đề số 6 – Đề kiểm tra học kì 2 – Toán 9

Câu I: 

Cho hai biểu thức \(A = \dfrac{{\sqrt x }}{{1 + 3\sqrt x }}\) và \(B = \dfrac{{x + 3}}{{x - 9}} + \dfrac{2}{{\sqrt x  + 3}} - \dfrac{1}{{3 - \sqrt x }}\) với \(x \ge 0;x \ne 9\)

a) Tính giá trị của biểu thức A khi \(x = \dfrac{4}{9}\)

b) Rút gọn biểu thức B

c) Cho \(P = B:A.\) Tìm x để P < 3.

Câu II:  Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình

Hai công nhân cùng làm chung một công việc thì trong 8 giờ xong việc. Nếu mỗi người làm một mình, để hoàn thành công việc đó thì người thứ nhất cần nhiều hơn người thứ hai là 12 giờ. Hỏi nếu làm một mình thì mỗi người phải làm trong bao nhiêu giờ xong công việc đó?

Câu III: 

1) Giải hệ phương trình \(\left\{ \begin{array}{l}\dfrac{1}{{2x - 1}} + \dfrac{4}{{y + 5}} = 3\\\dfrac{3}{{2x - 1}} - \dfrac{2}{{y + 5}} =  - 5\end{array} \right.\)

2) Cho phương trình \({x^2} - 2(m + 1)x + 2m = 0\) (1) (x là ẩn số, m là tham số)

a) Chứng minh phương trình (1) luôn có hai nghiệm phân biệt với mọi m

b) Gọi hai nghiệm của phương trình (1) là \({x_1},\) \({x_2}\). Tìm giá trị của m để \({x_1},\) \({x_2}\) là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng \(\sqrt {12} \).

Câu IV:  Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E bất kỳ (E khác A và C). Kẻ CK vuông góc với AE tại K. Đường thẳng DE cắt CK tại F.

a) Chứng minh tứ giác AHCK là tứ giác nội tiếp

b) Chứng minh KH song song với ED và tam giác ACF là tam giác cân.

c) Tìm vị trí của điểm E để diện tích tam giác ADF lớn nhất.

Câu V:  Giải phương trình \(\sqrt {5{x^2} + 4x}  - \sqrt {{x^2} - 3x - 18}  = 5\sqrt x \)

Câu I:

a)

* Khi \(x = \dfrac{4}{9}\) thì \(\sqrt x  = \dfrac{2}{3}\) thì \(A = \dfrac{{\dfrac{2}{3}}}{{1 + 3.\dfrac{2}{3}}} = \dfrac{2}{9}\)

* Vậy khi \(x = \dfrac{4}{9}\) thì \(A = \dfrac{2}{7}\)

b)

\(B = \dfrac{{x + 3}}{{x - 9}} + \dfrac{2}{{\sqrt x  + 3}} - \dfrac{1}{{3 - \sqrt x }}\)

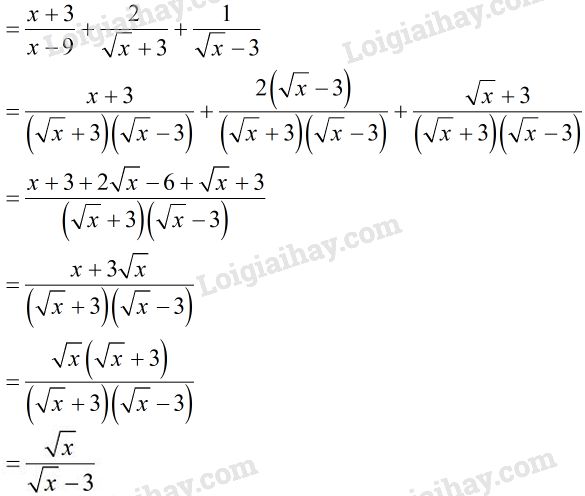
c)

Ta có: \(P = \dfrac{{\sqrt x }}{{\sqrt x  - 3}}:\dfrac{{\sqrt x }}{{1 + 3\sqrt x }} = \dfrac{{3\sqrt x  + 1}}{{\sqrt x  - 3}}\)

\(P < 3 \Leftrightarrow \dfrac{{3\sqrt x  + 1}}{{\sqrt x  - 3}} < 3\)

         \(\begin{array}{l} \Leftrightarrow \dfrac{{3\sqrt x  + 1}}{{\sqrt x  - 3}} - \dfrac{{3\left( {\sqrt x  - 3} \right)}}{{\sqrt x  - 3}} < 0\\ \Leftrightarrow \dfrac{{3\sqrt x  + 1 - 3\sqrt x  + 9}}{{\sqrt x  - 3}} < 0\\ \Leftrightarrow \dfrac{{10}}{{\sqrt x  - 3}} < 0\\ \Leftrightarrow \sqrt x  - 3 < 0\\ \Leftrightarrow \sqrt x  < 3\\ \Leftrightarrow x < 9\end{array}\)

Kết hợp điều kiện xác định duy ra \(0 < x < 9\) thì \(P < 3\)

Câu II:

Giả sử người thứ nhất làm riêng trong x (giờ) thì hoàn thành công việc (ĐK: x > 0)

Giả sử người thứ hai làm riêng trong y (giờ) thì hoàn thành công việc (ĐK: y > 0, y < x)

Trong 1 giờ người thứ nhất làm được \(\dfrac{1}{x}\) công việc

Trong 1 giờ người thứ hai làm được \(\dfrac{1}{y}\) công việc

Theo giả thiết, hai người làm chung thì hoàn thành công việc trong 8 giờ nên ta có:

                          \(\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{8}\) (1)

Khi làm riêng thì người thứ nhất cần nhiều hơn người thứ hai là 12 giờ để hoàn thành công việc nên ta có: \(x - y = 12\) (2)

Từ (1) và (2) ta có hệ phương trình

\(\begin{array}{l}\left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{{18}}\\x - y = 12\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}8\left( {2y + 12} \right) = xy\\x = y + 12\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}8(2y + 12) = y(y + 12)\\x = y + 12\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{y^2} - 4y - 96 = 0\\x = y + 12\end{array} \right.\end{array}\)

* Giải phương trình \({y^2} - 4y - 96 = 0\)

\( \Leftrightarrow \left( {y - 12} \right)\left( {y + 8} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}y = 12(TM)\\y =  - 8(L)\end{array} \right.\)

Từ đó suy ra x = 24.

Vậy nếu làm riêng thì người thứ nhất cần 12 giờ để hoàn thành công việc, người thứ hai cần 24 giờ để hoàn thành công việc.

Câu III:

1)

* ĐK: \(x \ne \dfrac{1}{2};y \ne  - 5\)

* Đặt \(\left\{ \begin{array}{l}\dfrac{1}{{2x - 1}} = a\\\dfrac{1}{{y + 5}} = b\end{array} \right.\), ta có hệ pt:

\(\left\{ \begin{array}{l}a + 4b = 3\\3a - 2b =  - 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a + 4b = 3\\6a - 4b =  - 10\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}7a =  - 7\\a + 4b = 3\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}a =  - 1\\b = 1\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}\dfrac{1}{{2x - 1}} =  - 1\\\dfrac{1}{{y + 5}} = 1\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}2x - 1 =  - 1\\y + 5 = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y =  - 1\end{array} \right.(TM)\) 

Vậy hệ có nghiệm (x.y) = (0;4)

2)

a)

Xét phương trình \({x^2} - 2(m - 1)x + 2m = 0\). Ta có \(\Delta ' = {(m + 1)^2} - 2m = {m^2} + 1\) vì \({m^2} \ge 0\) với mọi m nên \(\Delta ' \ge 1 > 0\) suy ra phương trình luôn có hai nghiệm phân biệt \({x_1},{x_2}\)

b)

Để 2 nghiệm \({x_1},{x_2}\)là độ dài 2 cạnh góc vuông của tam giác vuông có độ dài cạnh huyền bằng \(\sqrt {12} \) . Thì \({x_1},{x_2}\) là các số thực dương thỏa mãn \({x_1}^2 + {x_2}^2 = 12\)

Theo hệ thức Viet ta có : \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2(m + 1)\\{x_1}{x_2} = 2m\end{array} \right.\) để \({x_1},{x_2}\)>0 thì điều kiện là

\(\left\{ \begin{array}{l}2(m + 1) > 0\\2m > 0\end{array} \right. \Leftrightarrow m > 0\) hệ thức  \({x_1}^2 + {x_2}^2 = 12\) \( \Leftrightarrow \) (m - 1)(m - 2) = 0

\( \Leftrightarrow \)\(\left\{ \begin{array}{l}m = 1\\m =  - 2\end{array} \right.\) đối chiếu với điều kiện ta thấy m = 1 thỏa mãn.

Câu IV:

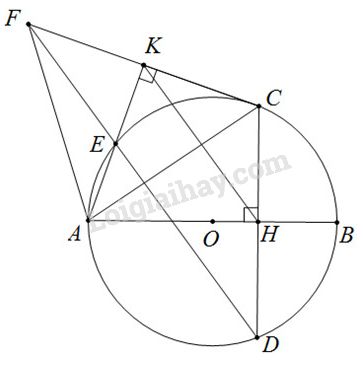
a)

Vì \(CK \bot AK\) nên \(\widehat {AKC} = {90^0}\). \(CH \bot AB\) tại H nên \(\widehat {AHC} = {90^0}\) . Tứ giác AHCK có :

\(\widehat {AHC} + \widehat {AKC} = {180^0}\)nên ACHK là tứ giác nội tiếp.

(Tổng 2 góc đối bằng \({180^0}\) ).

b)

Từ CHAK là tứ giác nội tiếp ta suy ra  \(\widehat {CHK} = \widehat {CAK} = \widehat {CAE}\) (góc nội tiếp cùng chắn cung KC).

Lại có ADCE nội tiếp nên \(\widehat {CAE} = \widehat {CDE}\)  (góc  nội tiếp cùng chắn cung EC).

Từ đó suy ra \(\widehat {CHK} = \widehat {CDE} \Rightarrow HK//DE\) .

Do HK// DF, mà H là trung điểm CD (Được suy ra từ quan hệ vuông góc của đường kính AB với dây CD tại H ).

Suy ra HK là đường trung bình của tam giác CDF, dẫn đến K là trung điểm FC. Tam giác AFC có AK là đường cao đồng thời cũng là trung tuyến nên CAF là tam giác cân tại K .

c)

Tam giác FAC cân tại A nên AF = AC.

Dễ thấy tam giác ACD cân tại A nên AC=AD từ đó suy ra AF =AD hay tam giác AFD cân tại A, hạ \(DI \bot {\rm{AF}}\) .

Ta có \({S_{AFD}} = \dfrac{1}{2}DI.{\rm{AF = }}\dfrac{1}{2}DI.AC,\) do AC không đổi nên \({S_{AFD}}\) lớn nhất khi và chỉ khi DI lớn nhất, Trong tam giác vuông AID ta có:

\(ID \le AD = AC\) hay \({S_{AFD}} = \dfrac{1}{2}DI.{\rm{AF = }}\dfrac{1}{2}DI.AC\)\(\, \le \dfrac{{A{C^2}}}{2}\) dấu đẳng thức xảy ra khi và chỉ khi \(I \equiv A\)  khi đó \(\widehat {DAF} = {90^0}\) dẫn đến tam giác ADF vuông cân tại A, suy ra \(\widehat {EBA} = \widehat {EDA} = {45^0}\) hay E là điểm chính giữa cung AB.

Câu V:

Điều kiện: \(\left\{ \begin{array}{l}{x^2} - 3x - 18 \ge 0\\x \ge 0\\5{x^2} + 4x \ge 0\end{array} \right. \Leftrightarrow x \ge 6\) .

PT \( \Leftrightarrow \sqrt {5{x^2} + 4x}  = \sqrt {{x^2} - 3x - 18}  \)\(\,+ 5\sqrt x \)

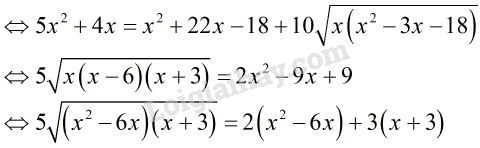
Đặt \(\left\{ \begin{array}{l}a = \sqrt {{x^2} - 6x}  \ge 0\\b = \sqrt {x + 3}  \ge 3\end{array} \right. \)

\(\Rightarrow 2{a^2} + 3{b^2} - 5ab = 0\)

\(\Leftrightarrow \left( {a - b} \right)\left( {2a - 3b} \right) = 0\)

* TH1: \(a = b \Leftrightarrow {x^2} - 6x = x + 3 \)

\(\Leftrightarrow {x^2} - 7x - 3 = 0 \)

\(\Leftrightarrow x = \dfrac{{7 + \sqrt {61} }}{2}\)

* TH2: \(2a = 3b \Leftrightarrow 4\left( {{x^2} - 6x} \right) = 9\left( {x + 3} \right)\)

\(\Leftrightarrow 4{x^2} - 33x - 27 = 0 \Leftrightarrow x = 9\)