a) Ta có công thức \({S_{xq}} = 2\pi rl\) với r = 50 cm, l = 50 cm.
Do đó \({S_{xq}} = 2\pi .50.50 = \pi .5000(c{m^2})\) và \(V = \pi {r^2}h = 125000.\pi (c{m^3})\)
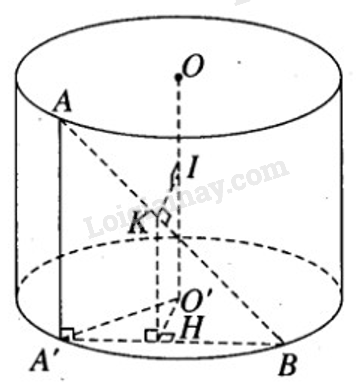
b) Giả sử đoạn thẳng AB có điểm mút A nằm trên đường tròn đáy tâm O’ .
Theo giả thiết ta có: AB = 100 cm. Giả sử IK là đoạn vuông góc chung của trục OO’ và đoạn AB với I thuộc OO’ và K thuộc AB.
Chiếu vuông góc đoạn AB xuống mặt phẳng đáy chứa đường tròn tâm O’ , ta có A’ , H , B lần lượt là hình chiếu của A, K, B.
Vì \(KI \bot OO'\) nên IK // mp(O’BA’) , do đó O’H // IK và O’H = IK.
Ta suy ra \(O'H \bot AB\) và \(O'H \bot AA'\) . Vậy \(O'H \bot A'B\)
Xét tam giác vuông AA’B ta có \(A'B = \sqrt {A{B^2} - AA{'^2}} = \sqrt {{{100}^2} - {{50}^2}} = 50\sqrt 3 \)
Vậy \(IK = O'H = \sqrt {O'{A^2} - A'{H^2}}\)
\( = \sqrt {{{50}^2} - {{({{50\sqrt 3 } \over 2})}^2}} = 50\sqrt {1 - {3 \over 4}} = 25(cm)\)