Bài 3. Đường thẳng đi qua hai điểm

Đề bài

Cho ba điểm \(A, B, C\) không thẳng hàng. Kẻ các đường thẳng đi qua các cặp điểm:

a) Kẻ được mấy đường thẳng tất cả?

b) Viết tên các đường thẳng đó.

c) Viết tên giao điểm của từng cặp đường thẳng.

Đề bài

Vẽ đường thẳng \(a.\) Lấy \(A ∈ a, B ∈ a, C ∈ a, D\) không thuộc \(a.\) Kẻ các đường thẳng đi qua các cặp điểm.

a) Kẻ được tất cả bao nhiêu đường thẳng (phân biệt)?

b) Viết tên các đường thẳng đó.

c) \(D\) là giao điểm của những đường thẳng nào?

Đề bài

Cho ba đường thẳng. Vẽ hình trong các trường hợp sau:

a) Chúng có 1 giao điểm.

b) Chúng có ba giao điểm. 

c) Chúng không có giao điểm nào.

Đề bài

Vẽ bốn đường thẳng cắt nhau từng đôi một trong các trường hợp sau:

a) Chúng có tất cả 1 giao điểm.

b) Chúng có tất cả 4 giao điểm.

c) Chúng có tất cả 6 giao điểm.

Đề bài

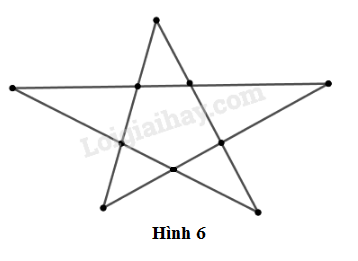
Vẽ sao năm cánh như hình 6.

a) Đặt tên cho các giao điểm trên hình 6.

b) Đọc tên các bộ bốn điểm thẳng hàng.

c) Năm đường thẳng cắt nhau từng đôi một cho nhiều nhất mấy giao điểm?

d) Vẽ một hình khác có 5 đường thẳng cắt nhau từng đôi một và cho 10 giao điểm.

Đề bài

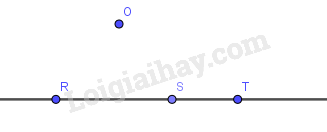
Xem hình 7 và dùng các ký hiệu \(∈\) hoặc \(\notin \) để điền vào chỗ trống cho thích hợp.

\(O….\) Đường thẳng \(RS\)

\(R….\) Đường thẳng \(ST\)

\(S….\) Đường thẳng \(OT\)

\(T…. \) Đường thẳng \(SR\)

Đề bài

Mỗi câu sau đây là đúng hay sai?

a) Có một và chỉ một đường thẳng đi qua hai điểm (phân biệt) cho trước.

b) Có đúng ba đường thẳng đi qua ba điểm (phân biệt) cho trước.

c) Có đúng sáu đường thẳng đi qua bốn điểm (phân biệt) cho trước.

d) Hai đường thẳng phân biệt thì song song với nhau.

e) Hai đường thẳng không cắt nhau thì song song. 

f) Hai đường thẳng không song song thì cắt nhau.

g) Hai đường thẳng không phân biệt thì trùng nhau.

h) Ba đường thẳng phân biệt, đôi một cắt nhau thì có đúng 3 giao điểm (phân biệt).

Đề bài

Vẽ từng hình theo mỗi cách diễn đạt sau đây

a) Hai đường thẳng có chỉ một điểm chung.

b) Hai đường thẳng có đúng hai điểm chung.

c) Hai đường thẳng có đúng ba điểm chung.

d) Hai đường thẳng không song song với nhau.

Đề bài

Cho biết có thể vẽ được bao nhiêu đường thẳng (phân biệt) trong mỗi trường hợp sau:

a) Với hai điểm (phân biệt) cho trước.

b) Với ba điểm (phân biệt) cho trước và không thẳng hàng.

c) Với bốn điểm (phân biệt) cho trước, trong đó không có 3 điểm nào thẳng hàng.