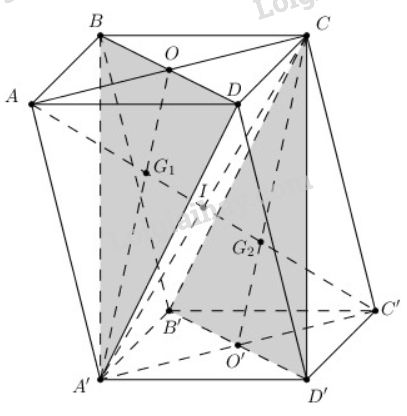
a) Ta có: \(BB'//DD'; BB'=DD' \Rightarrow\) \(BDD'B'\) là hình bình hành \(\Rightarrow BD//B'D'\).
\(BC//A'D';BC=A'D' \Rightarrow BCD'A'\) là hình bình hành \(\Rightarrow A'B//CD'\).
\(\Rightarrow (BDA')//(B'D'C)\).
b) Gọi \(O,O'\) lần lượt là tâm của hình bình hành \(ABCD,A'B'C'D'\), \({G_{1}}^{}\), \({G_{2}}^{}\) là giao điểm của \(AC'\) với \(A'O\) và \(CO'\)
\(\Delta {G_1}OA\) đồng dạng \(\Delta {G_1}A'C'\) (g.g)
\( \Rightarrow {{{G_1}O} \over {{G_1}A'}} = {{OA} \over {A'C'}} = {1 \over 2} \Rightarrow {{A'{G_1}} \over {A'O}} = {2 \over 3}\).
Lại có \({G_1} \in A'O\) là đường trung tuyến của \(\Delta BDA'\) \(\Rightarrow G_1\) là trọng tâm \(\Delta A'BD\).
Chứng minh tương tự ta có: \(G_2\) là trọng tâm \(\Delta B'D'C\).
Vậy \(AC'\) đi qua \(G_1,G_2\) lần lượt là trọng tâm của hai tam giác \(BDA'\) và \(B'D'C\).
c) Chứng minh
\( \frac{A{G_{1}}^{}}{{G_{1}C'}}\) = \( \frac{AO}{A'C'} = \frac{1}{2}\) (vì \(\Delta G_1OA\) đồng dạng \(\Delta G_1 A'C'\)) \( \Rightarrow A{G_1} = \frac{1}{3}AC'\).
Từ đó suy ra: \( {AG_{1} = {G_{1}{G_{2}= {G_{2}C'}^{}}^{}}^{}}^{}\)
d) \((A'IO) ≡ (AA'C'C)\) suy ra thiết diện của hình hộp khi cắt bởi mặt phẳng \((A'IO)\) là \(AA'C'C\).