a - S
b - S
c - S
d - S
e - S
Góc đó có thể là góc vuông hoặc góc bẹt.
f - S
Góc đó có thể là góc nhọn hoặc góc bẹt.
g - S
Góc đó có thể là góc nhọn hoặc góc vuông.
h - Đ
i - Đ.
Bài 3.2
Cho hình bs.4
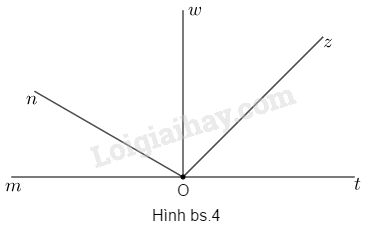
a) Hãy đọc tên các góc đỉnh \(O\) có trong hình đó;
b) Cho biết số đo của góc nhọn đỉnh \(O\), một cạnh là \(Ot\) có trong hình đó;
c) Cho biết số đo của góc nhọn đỉnh \(O\), một cạnh \(Om\) có trong hình đó;
d) Hãy đo và cho biết tên của các góc vuông đỉnh \(O\) có trong hình đó;
e) Cho biết số đo của các góc tù đỉnh \(O\) có trong hình đó;
f) Hãy đo và cho biết tên của góc bẹt đỉnh \(O\) có trong hình đó.
a) Ta có các góc đỉnh \(O\) là: \(mOt, mOz, mOw,\) \(mOn, nOt, nOz, \) \(nOw, wOt, wOz, zOt.\)
b) \(\widehat {tOz} = 45^\circ \)
c) \(\widehat {mOn} = 30^\circ \)
d) \(\widehat {m{{Ow}}} = 90^\circ \) và \(\widehat {{{tOw}}} = 90^\circ \)
e) \(\widehat {tOn} = 150^\circ \) và \(\widehat {mOz} = 135^\circ \)
f) \(\widehat {tOm} = 180^\circ \).
Bài 3.3
a) Hai đường thẳng \(xx’, yy’ \) cắt nhai tại điểm \(O\) và \(\widehat {xOy} = 90^\circ \). Hãy đo và cho biết số đo của các góc \(yOx’, x’Oy’, y’Ox.\)
b) Hai đường thẳng \(xx’, yy’\) cắt nhai tại điểm \(O\) và \(\widehat {xOy} = 30^\circ \). Hãy đo và cho biết số đo của các góc \(yOx’, x’Oy’, y’Ox.\)
a)
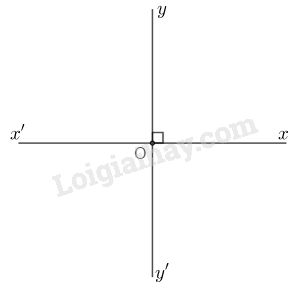
Các góc \(yOx’, x’Oy’, y’Ox\) đều có số đo bằng \(90^\circ \).
b)
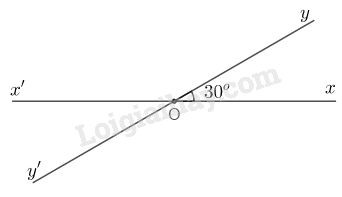
Đo các góc ta được:
\(\widehat {x'Oy'} = 30^\circ ,\widehat {x'Oy} = 150^\circ ,\) \(\widehat {xOy'} = 150^\circ \).
Phương pháp giải Sử dụng:
- Góc có số đo bằng \(90^0\) là góc vuông.
- Góc có số đo nhỏ hơn \(90^0\) độ là góc nhọn.
- Góc có số đo lớn hơn góc vuông nhưng nhỏ hơn góc bẹt là góc tù.
- Góc có số đo bằng \(180^0\) là góc bẹt.

* Cách đo góc \(xOy\)
- Bước 1: Đặt thước đo góc sao cho tâm của thuốc trùng với tâm \(O\) của góc, một cạnh của góc đi qua vạch \(0^0\)
- Bước 2: Xem cạnh thứ hai của góc đi qua vạch nào của thước, giả sử là vạch \(120^0\) thì viết là \(\widehat{xOy}=120^o\).