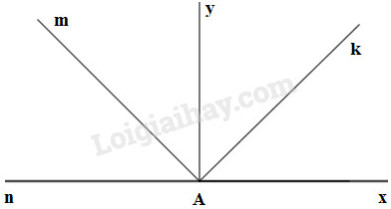
Bài 5.2
Vẽ từng hình theo mỗi cách diễn đạt sau:
a) Hai góc \(xOy\) và \(yOz\) kề bù, với \(\widehat {xOy} = 135^\circ .\)
b) Hai góc \(mOn\) và \(nOt\) kề nhau và phụ nhau, với \(\widehat {nOm} = 30^\circ .\)
c) Cho tia \(Ap\). Vẽ \(\widehat {qAp} = 30^\circ. \)
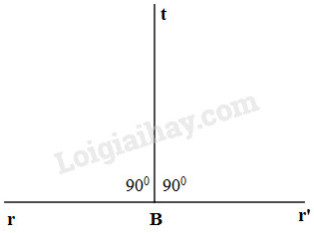
d) Cho tia \(Ck\). Vẽ \(\widehat {rBt} = 90^\circ .\)
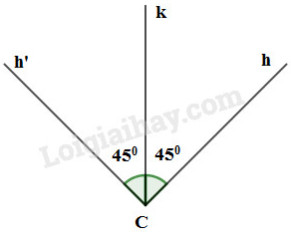
e) Cho tia \(Ck\). Vẽ \(\widehat {hCk} = 45^\circ. \)
Lưu ý : Bài tập dạng này có nhiều trường hợp về hình vẽ. Chỉ yêu cầu HS vẽ đúng một trường hợp, riêng với các ý c, d, và e chú ý có 2 trường hợp về hình vẽ :
a)
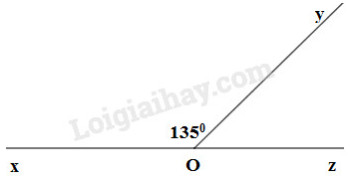
b)
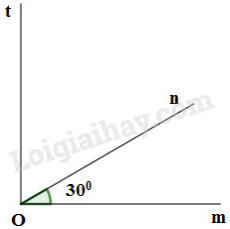
c)
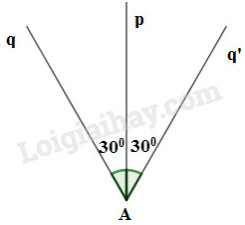
d)
e)
Bài 5.3
Vẽ \(\widehat {mOn} = 30^\circ \). Tiếp góc \(nOp\) kề bù với góc \(mOn\). Vẽ tiếp góc \(pOq\) phụ với góc \(mOn\) đồng thời tia \(Oq\) nằm trong góc \(nOp\). Cho biết số đo của góc \(nOq\).
Từ giả thiết ta vẽ được hình sau :
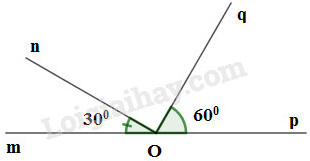
Vì góc \(nOp\) kề bù với góc \(mOn\) suy ra góc \(mOp\) là góc bẹt.
Vì \(\widehat {mOn} = 30^\circ \) và góc \(pOq\) phụ với góc \(mOn\) nên \(\widehat {pOq} = 60^\circ \)
Vì \(\widehat {mOn} = 30^\circ \) và góc \(nOp\) kề bù với góc \(mOn\) nên \(\widehat {nOp} = 150^\circ \)
Do tia \(Oq\) nằm trong góc \(nOp\) nên \(\widehat {nOp} = \widehat {nOq} + \widehat {qOp}\) hay \(\widehat {nOq} + 60^\circ = 150^\circ \). Từ đó \(\widehat {nOq} = 90^\circ \).
Phương pháp giải Dùng thước kẻ và đo độ để vẽ hình theo yêu cầu đề bài.
Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau. Hai góc kề bù có tổng số đo bằng \(180^0.\)
Hai góc kề nhau là hai góc có 1 cạnh chung.
Áp dụng các tính chất :
- Tổng hai góc kề bù bằng \(180^\circ.\)
- Nếu tia \(Oy\) nằm giữa tia \(Ox\) và tia \(Oz\) thì \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\).