Bài 7 trang 126 SGK Hình học 11

Cho hình thang \(ABCD\) vuông tại \(A\) và \(B\), có \(AD = 2a, AB = BC = a\). Trên tia \(Ax\) vuông góc với mặt phẳng \((ABCD)\) lấy một điểm \(S\). Gọi \(C',D'\) lần lượt là hình chiếu vuông góc của \(A\) trên \(SC\) và \(SD\) . Chứng minh rằng :

a) \(\widehat {SBC} = \widehat {SC{\rm{D}}} = {90^0}\)  

b) \(AD’,  AC’\) và \(AB\) cùng nằm trên một mặt phẳng.

c) Chứng minh rằng đường thẳng \(C’D’\) luôn luôn đi qua một điểm cố định khi \(S\) di động trên tia Ax.

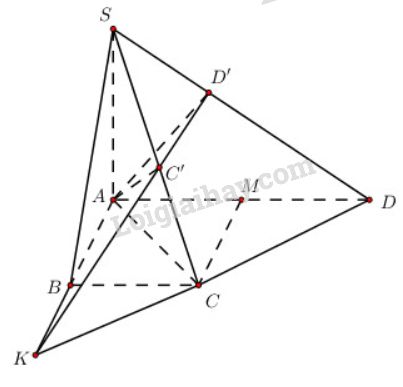
a) Ta có: \(\left. \matrix{SA \bot \left( {ABC{\rm{D}}} \right) \hfill \cr AB \bot BC \hfill \cr} \right\} \Rightarrow SB \bot BC\) (định lí 3 đường vuông góc) \( \Rightarrow \widehat {SBC} = {90^0}\) 

Gọi \(M\) là trung điểm của \(AD\).

\(ABCM\) là hình vuông nên \(CM = a  \Rightarrow CM = {1 \over 2}A{\rm{D}}\) 

Tam giác \(ACD\) có trung tuyến \(CM\) bằng \({1 \over 2}\) cạnh tương ứng nên nó là tam giác vuông, hay tam giác \(ACD\) vuông tại \(C\) có \(AC ⊥ CD\)

\(\left. \matrix{ SA \bot \left( {ABC{\rm{D}}} \right) \hfill \cr AC \bot C{\rm{D}} \hfill \cr} \right\} \Rightarrow SC \bot C{\rm{D}}\) (định lí 3 đường vuông góc)

\(\Rightarrow \widehat {SC{\rm{D}}} = {90^0}\)

b) Ta có :

\(\left. \matrix{ AB \bot SA \hfill \cr AB \bot A{\rm{D}} \hfill \cr} \right\} \Rightarrow \left. \matrix{ AB \bot \left( {SA{\rm{D}}} \right) \hfill \cr S{\rm{D}} \subset \left( {SA{\rm{D}}} \right) \hfill \cr} \right\} \Rightarrow AB \bot S{\rm{D}}\,\,\,\,\,(1)\)

\(\left. \matrix{ C{\rm{D}} \bot AC \hfill \cr C{\rm{D}} \bot SC \hfill \cr} \right\} \Rightarrow \left. \matrix{ C{\rm{D}} \bot \left( {SAC} \right) \hfill \cr AC' \subset \left( {SAC} \right) \hfill \cr} \right\} \Rightarrow AC' \bot C{\rm{D}}\)

Kết hợp với \( AC’ ⊥ SC\) suy ra \(AC'\bot (SCD)\)

\(\Rightarrow \left. \matrix{AC' \bot \left( {SC{\rm{D}}} \right) \hfill \cr S{\rm{D}} \subset \left( {SC{\rm{D}}} \right) \hfill \cr} \right\} \Rightarrow AC' \bot S{\rm{D\,\,\,\,\,(2)}}\)

Giả thiết cho \(AD’ ⊥ SD\)    (3)

Từ (1), (2), (3) ta thấy ba đường thẳng \(AB, AD’, AC’\) cùng vuông góc với \(SD\). Vậy chúng cùng nằm trong mặt phẳng \(( P)\) đi qua \(A\) và vuông góc với \(SD\).

c) Gọi \(K\) là giao điểm của \(C’D’\) với \(AB\).

\(K ∈ C’D’ ⇒ K ∈ (SCD)\)

\(K  ∈ AB ⇒ K ∈ (ABCD)\)

\(⇒ K\) là giao điểm của hai mặt phẳng \((SCD)\) và \((ABCD)\)

Hai mặt phẳng này cắt nhau theo giao tuyến \(CD\). Như vậy ba đường thẳng \(AB, CD, C’D’\) đồng quy tại \(K\) và \(AB, CD\) cố định suy ra \(K\) cố đinh.

Khi \(S\) chạy trên \(Ax\) thì \(C’D’\) luôn đi qua điểm cố định là giao điểm của \(AB\) và \(CD\).