a.
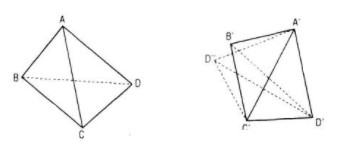
Giả sử hai tứ giác lồi ABCD và A’B’C’D’ có \(AB = A’B’; BC = B’C’; CD = C’D’, DA = D’A’\) và \(AC = A’C’\)
Khi đó hai tam giác ABC và A’B’C’ bằng nhau nên có phép dời hình F biến ba điểm A, B, C lần lượt thành ba điểm A’, B’, C’
Gọi D” là điểm đối xứng với điểm D’ qua đường thẳng A’C’ thì hai tam giác A’C’D’ và A’C’D” bằng nhau và theo giả thiết, cùng bằng tam giác ACD
Bởi vậy phép F chỉ có thể biến điểm D thành điểm D’ hoặc D” (do phép dời hình bảo toàn độ dài đoạn thẳng)
Vì ABCD là tứ giác lồi nên hai đoạn thẳng AC và BD cắt nhau, A’B’C’D’ cũng là tứ giác lồi nên hai đoạn thẳng nên hai đoạn thẳng A’C’ và B’D’ cắt nhau, và do đó hai đoạn thẳng A’C’ và B’D” không cắt nhau
Từ đó ta suy ra F biến D thành D’
Vậy F biến tứ giác ABCD thành tứ giác A’B’C’D’ và do đó hai tứ giác đó bằng nhau
b. Giả sử hai tứ giác ABCD và A’B’C’D’ có \(AB = A’B’, BC = B’C’, CD = C’D’, DA = D’A’\) và góc ABC bằng góc A’B’C’
Khi đó \(AC = A’C’\) và ta đưa về trường hợp ở câu a)
c. Có thể không bằng nhau
Hai hình thoi có cạnh bằng nhau nhưng có thể là hai hình không bằng nhau (vì phép dời hình biến góc thành góc bằng nó)