Câu C1 trang 117 SGK Vật lý 12

Điền kí hiệu (∈, ∉, ⊂, ∩) thích hợp vào ô vuông:

\(\displaystyle {{ - 3} \over 4}\, \square \, {\rm{ }}Z;\)                       \(0 \, \square \, N ;\)                       \(3,275 \, \square \, N;\) 

\(N \, \square \, Z = N; \)                     \(N \, \square \, Z.\) 

Điền vào chỗ trống:

a) Với \(a, n ∈ N\)

\({a^n} = \underbrace {a.a.a.\,...\,.a}_{...\,\,thừa\,\,số}\) với \(...\)

Với \(a ≠ 0\) thì \(a^0= ...\)

b) Với \(a, m, n ∈ N\)

\({a^m}.{a^n} =...\)

\({a^m}:{a^n} = ...\) với ..... 

Tìm giao của tập hợp C các số chẵn và tập hợp L các số lẻ. 

Tính giá trị các biểu thức sau:

\(A = 27 + 46 + 79 + 34 + 53;\)

\(B = - 377 - (98 - 277)\)

\(C = - 1,7× 2,3 + 1,7× (- 3,7) - 1,7×3 - 0,17:0,1\)

\(\displaystyle D = 2{3 \over 4}.\left( { - 0,4} \right) - 1{3 \over 5}.2,75 + \left( { - 1,2} \right):{4 \over {11}}\)

\(E = \displaystyle {{\left( {{2^3}.5.7} \right)\left( {{5^2}{{.7}^3}} \right)} \over {{{\left( {{{2.5.7}^2}} \right)}^2}}}\)

Chia đều \(60\) chiếc kẹo cho tất cả học sinh lớp 6C thì còn dư \(13\) chiếc. Hỏi lớp 6C có bao nhiêu học sinh? 

Một ca nô xuôi một khúc sông hết \(3\) giờ và ngược khúc sông đó hết \(5\) giờ. Biết vận tốc dòng nước là \(3\) km/h. Tính độ dài khúc sông đó.

So sánh hai biểu thức A và B biết rằng:

\( \displaystyle A = {{2000} \over {2001}} + {{2001} \over {2002}}\)

\( \displaystyle B = {{2000 + 2001} \over {2001 + 2002}}\) 

Hai vòi nước cùng chảy vào một bể. Biết rằng để chảy được nửa bể, một mình vòi A phải mất 4 giờ 30 phút còn một mình vòi B chỉ mất 2 giờ 15 phút. Hỏi cả hai vòi cùng chảy vào bể đó thì sau bao lâu bể sẽ đầy? 

Tính:

a) \( \displaystyle 1{{13} \over {15}}.{\left( {0,5} \right)^2}.3 + \left( {{8 \over {15}} - 1{{19} \over {60}}} \right):1{{23} \over {24}}\)

b) \(\dfrac{{\left( {\dfrac{{{{11}^2}}}{{200}} + 0,415} \right):0,01}}{{\dfrac{1}{{12}} - 37,25 + 3\dfrac{1}{6}}}\)

Độ C và độ F

Ở nước ta và nhiều nước khác, nhiệt độ được tính theo độ C (chữ dầu của Celsius, đọc là Xen – xi - ớt – xơ ).

Ở Anh, Mỹ và một số nước khác, nhiệt độ được tính theo độ F (chữ đầu của Fahrenheit, đọc là Phe – rơn – hai – tơ). Công thức đổi từ độ C sang độ F là: \(F = \dfrac{9}{5}C + 32\)

(F và C ở đây là số độ F và số độ C tương ứng). 

a) Tính xem trong điều kiện bình thường, nước sôi ở bao nhiêu độ F?

b) Lập công thức đổi từ độ F sang độ C rồi tính xem \(50^\circ F\) tương đương với bao nhiêu độ C?

c) Ở Bắc cực có một thời điểm mà nhiệt kế đo độ C và nhiệt kế đo độ F cùng chỉ một số. Tìm số đó.

“Tỉ số vàng”

Người Cổ Hy Lạp và người Cổ Ai Cập đã ý thức được tỉ số “đẹp” trong các công trình xây dựng. Họ cho rằng hình chữ nhật đẹp là hình chữ nhật có tỉ số giữa chiều dài và chiều rộng là \(1: 0,618\) (các hình chữ nhật: DPLC, APLB, HGLB, … trong hình 17). Vì thê, tỉ số này được gọi là “tỉ số vàng” (theo cách gọi của nhà danh họa và nhà khoa học người Ý nổi tiếng Lê – ô – nác – đô đa Vin – xi). 

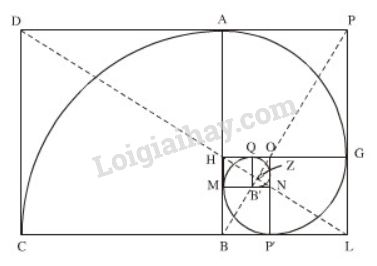
Khi nghiên cứu kiến trúc của Đền cổ Pác – tê – nông (h.18) ở A – ten (Hy Lạp), người ta nhận xét kích thước của các hình hình học trong đền phần lớn chịu ảnh hưởng của “tỉ số vàng”.

a) Các kích thước của một hình chữ nhật tuân theo “tỉ số vàng”, biết rằng chiều rộng của nó đo được 3,09m. Tính chiều dài của hình chữ nhật đó.

b) Chiều dài của một hình chữ nhật là 4,5 m. Để có “tỉ số vàng” thì chiều rộng của nó phải là bao nhiêu?

c) Một khu vườn hình chữ nhật có chiều dài là 15,4m, chiều rộng là 8m. Khu vườn này có đạt “tỉ số vàng” không?