Bài 1:
\(a)\dfrac{{ - 10}}{{13}} + \dfrac{5}{{17}} - \dfrac{3}{{13}} + \dfrac{{12}}{{17}} - \dfrac{{11}}{{20}}\)
\( = \left( {\dfrac{{ - 10}}{{13}} - \dfrac{3}{{13}}} \right) + \left( {\dfrac{5}{{17}} + \dfrac{{12}}{{17}}} \right) \)\(\;- \dfrac{{11}}{{20}}\)
\( = ( - 1) + 1 - \dfrac{{11}}{{20}}\)
\( = - \dfrac{{11}}{{20}}\)
\(b)\dfrac{3}{4} + \dfrac{{ - 5}}{6} - \dfrac{{11}}{{ - 12}}\)
\( = \dfrac{{9 + ( - 10) + 11}}{{12}}\)
\( = \dfrac{{10}}{{12}}\)
\(= \dfrac{5}{6}\)
\(c)\;\,\left( {\,13\dfrac{4}{9} + 2\dfrac{1}{9}} \right)\, - 3\dfrac{4}{9}\)
\( = \,\left( {\,13\dfrac{4}{9} - 3\dfrac{4}{9}} \right) + 2\dfrac{1}{9}\)
\( = \,10 + 2\dfrac{1}{9}\)
\( = \,12\dfrac{1}{9}\)
\(d)1,25:\dfrac{{15}}{{20}} + \left( {25\% - \dfrac{5}{6}} \right):4\dfrac{2}{3}\)
\( = \dfrac{5}{4}.\dfrac{4}{3} + \left( {\dfrac{1}{4} - \dfrac{5}{6}} \right).\dfrac{3}{{14}}\)
\( = \dfrac{5}{3} + \dfrac{7}{{12}}.\dfrac{3}{{14}}\)
\( = \dfrac{5}{3} + \dfrac{{ - 1}}{8} = \dfrac{{37}}{{24}}\)
Bài 2:
\({\text{a}})x - \dfrac{1}{3} = \dfrac{5}{{14}}.\dfrac{{ - 7}}{6}\)
\(x - \dfrac{1}{3} = \dfrac{{ - 5}}{{12}}\)
\(x = \dfrac{{ - 5}}{{12}} + \dfrac{1}{3}\)
\(x = \dfrac{{ - 1}}{{12}}\)
\(b)\;\dfrac{3}{4} + \dfrac{1}{4}.x = 0,2\)
\(\dfrac{1}{4}.x = \dfrac{1}{5} - \dfrac{3}{4}\)
\(\dfrac{1}{4}x = \dfrac{{ - 11}}{{20}}\)
\(x = \dfrac{{ - 11}}{5}\)
\(\eqalign{ & c)\,\,{1 \over {12}}{x^2} = 1{1 \over 3} \cr& \,\,\,\,\,{x^2} = {4 \over 3}:{1 \over {12}} \cr& \,\,\,\,\,\,{x^2} = {4 \over 3}.{{12} \over 1} = 16 \cr & \,\,\,\,\,\,\,x = \pm 4 \cr} \)
Bài 3:
a) Số học sinh chọn đi Đầm Long: \(45.\dfrac{1}{3} = 15(hs)\)
Số học sinh chọn đi Khoang Xanh: \((45 - 15).\dfrac{2}{3} = 20(hs)\)
Số học sinh chọn đi Đảo Ngọc Xanh: \(45 - (15 + 20) = 10(hs)\)
Số học sinh chọn đi Khoang Xanh là nhiều nhất
b) Tỉ số phần trăm số học sinh chọn đi Đảo Ngọc Xanh so với học sinh cả lớp : \(\dfrac{{10.100}}{{45}}\% = 22,22\% \)
Bài 4:
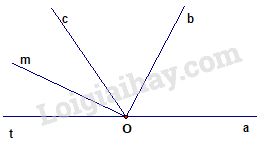
a) Vì tia Ob, Oc cùng một nửa mặt phẳng bờ chứa tia Oa, và \(\widehat {aOb} < \widehat {aOc}\left( {{{60}^o} < {{120}^o}} \right)\) nên tia Ob nằm giữa hai tia Oa và Oc.Ta có:\(\widehat {bOc} = \widehat {aOc} - \widehat {aOb} = {120^o} - {60^o} = {60^0}\)
b) Ob là tia phân giác của \(\widehat {aOc}\) vì:
+) Ob nằm giữa tia Oa và Oc+) \(\widehat {aOb} = \widehat {bOc} = \dfrac{{\widehat {aOc}}}{2}( = {60^0}\)c) Vẽ tia Ot là tia đối của tia Oa và Om là tia phân giác của \(\widehat {cOt}\). Chứng tỏ: \(\widehat {bOc}\) và \(\widehat {cOm}\) phụ nhau.
Vì tia Ot là tia đối của tia Oa \( \Rightarrow \widehat {cOt} = {60^0}\)Tia Om là tia phân giác của \(\widehat {cOt}\) \( \Rightarrow \widehat {cOm} = {30^0}\)\(\widehat {bOc} + \widehat {cOm} = {90^0}\)\(\widehat {bOc};\widehat {cOm}\) là hai góc phụ nhau
Bài 5: