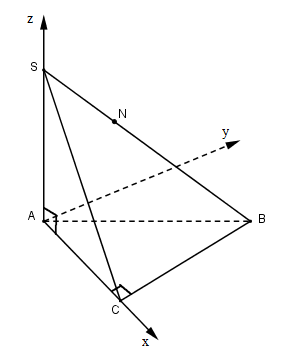
Chọn hệ trục Oxyz như hình vẽ, B nằm trong góc xOy.Ta có: \(A = \left( {0;0;0} \right),C = \left( {b;0;0} \right),B = \left( {b;a;0} \right),S = \left( {0;0;h} \right)\) .
\(M\left( {{b \over 2};0;0} \right),\overrightarrow {SB} = \left( {b;a; - h} \right)\)
Gọi \(N\left( {x;y;z} \right)\) thì \(\overrightarrow {SN} = \left( {x;y;z - h} \right)\).
\(\overrightarrow {SN} = {1 \over 3}\overrightarrow {SB} \Leftrightarrow \left\{ \matrix{ x = {b \over 3} \hfill \cr y = {a \over 3} \hfill \cr z - h = {{ - h} \over 3} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = {b \over 3} \hfill \cr y = {a \over 3} \hfill \cr z = {{2h} \over 3} \hfill \cr} \right. \Rightarrow N\left( {{b \over 3};{a \over 3};{{2h} \over 3}} \right)\)
a)
\(\eqalign{
& \overrightarrow {MN} = \left( {{b \over 3} - {b \over 2};{a \over 3};{{2h} \over 3}} \right) = \left( { - {b \over 6};{a \over 3};{{2h} \over 3}} \right) \cr
& MN = \sqrt {{{{b^2}} \over {36}} + {{{a^2}} \over 9} + {{4{h^2}} \over 9}} = {1 \over 6}\sqrt {{b^2} + 4{a^2} + 16{h^2}} \cr} \)
b) \(MN \bot SB \Leftrightarrow \overrightarrow {MN} .\overrightarrow {SB} = 0 \Leftrightarrow - {{{b^2}} \over 6} + {{{a^2}} \over 3} + {{ - 2{h^2}} \over 3} = 0 \Leftrightarrow 4{h^2} = 2{a^2} - {b^2}\)