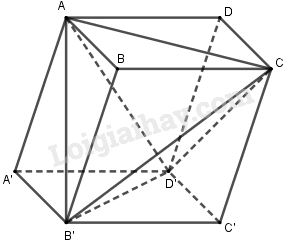
Đặt \(V = {V_{ABCD.A'B'C'D'}}\).
Ta có: \({V_{ACB'D'}} = V - {V_{A.A'B'D'}}\) \( - {V_{B'.BAC}} - {V_{C.C'B'D'}} - {V_{D'.ADC}}\)
Mà \({V_{A.A'B'D'}} = {V_{B'.BAC}}\) \( = {V_{C.C'B'D'}} = {V_{D'.ADC}} = \dfrac{1}{6}V\)
\( \Rightarrow {V_{ACB'D'}} = V - \dfrac{4}{6}V = \dfrac{1}{3}V\).
Vậy \(\dfrac{{{V_{ACB'D'}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{1}{3}\).