Bài 3: Khái niệm về thể tích khối đa diện

Cho khối chóp tam giác đều \(S.ABC\) có đáy là tam giác đều cạnh bằng \(a\), các cạnh bên tạo với đáy một góc \({60^0}\). Hãy tính thể tích của khối chóp đó.

Cho khối chóp \(S.ABC\) có đáy là tam giác cân, \(AB = AC = 5a,BC = 6a\) và các mặt bên tạo với đáy một góc \({60^0}\). Hãy tính thể tích của khối chóp đó.

Cho hình chóp tam giác \(S.ABC\) có đáy là tam giác vuông ở \(B\). Cạnh \(SA\) vuông góc với đáy. Từ \(A\) kẻ các đoạn thẳng \(AD\) vuông góc với \(SB\) và \(AE\) vuông góc với \(SC\). Biết rằng \(AB = a,BC = b,SA = c\).

a) Hãy tính thể tích khối chóp \(S.ADE\)

b) Tính khoảng cách từ \(E\) đến mặt phẳng \(\left( {SAB} \right)\).

LG câu a

Phương pháp:

- Chứng minh \(SE \bot \left( {ADE} \right)\).

- Tính diện tích tam giác \(ADE\) và chiều cao \(SE\).

- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\).

Cách giải:

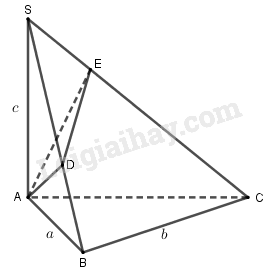
Ta có \(\left\{ {\begin{array}{*{20}{c}}{BC \bot SA}\\{BC \bot AB}\end{array}} \right. \Rightarrow BC \bot (SAB)\)

Vì \(AD \subset (SAB)\) nên \(AD \bot BC\)

Mặt khác \(AD \bot SB\) nên \(AD \bot (SBC)\)

Từ đó suy ra \(AD \bot SC\)

\(\left\{ {\begin{array}{*{20}{c}}{SC \bot AE}\\{SC \bot AD}\end{array}} \right.\)\( \Rightarrow SC \bot (ADE) \Rightarrow SC \bot DE\) hay \(SE \bot (ADE)\).

Trong tam giác vuông \(SAB\) ta có: \(SA.AB = AD.SB\)\( \Rightarrow AD = \dfrac{{AB.SA}}{{SB}} = \dfrac{{ac}}{{\sqrt {{a^2} + {c^2}} }}\)

Tương tự, trong tam giác vuông \(SAC\) ta có: \(AE = \dfrac{{SA.AC}}{{SC}} = \dfrac{{c\sqrt {{a^2} + {b^2}} }}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)

Do \(AD \bot (SBC)\)  nên \(AD \bot DE\). Từ đó suy ra:

\(DE = \sqrt {A{E^2} - A{D^2}} \)\( = \sqrt {\dfrac{{{c^2}({a^2} + {b^2})}}{{{a^2} + {b^2} + {c^2}}} - \dfrac{{{a^2}{c^2}}}{{{a^2} + {c^2}}}} \) \( = \dfrac{{{c^2}b}}{{\sqrt {({a^2} + {b^2} + {c^2})({a^2} + {c^2})} }}\)

\(SE = \sqrt {S{A^2} - A{E^2}} \)\( = \sqrt {{c^2} - \dfrac{{{c^2}({a^2} + {b^2})}}{{{a^2} + {b^2} + {c^2}}}} \) \( = \dfrac{{{c^2}}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)

Vậy \({V_{S.ADE}} = \dfrac{1}{3}.\dfrac{1}{2}AD.DE.SE\)\( = \dfrac{1}{6}\dfrac{{ac}}{{\sqrt {{a^2} + {c^2}} }}.\dfrac{{{c^2}b}}{{\sqrt {({a^2} + {b^2} + {c^2})({a^2} + {c^2})} }}.\dfrac{{{c^2}}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)

\( = \dfrac{{ab{c^5}}}{{6({a^2} + {b^2} + {c^2})({a^2} + {c^2})}}\)

LG câu b

Phương pháp:

- Tính diện tích tam giác \(SAD\).

- Sử dụng công thức \({V_{SADE}} = \dfrac{1}{3}d.{S_{SAD}}\) và kết quả câu a để suy ra \(d\).

Cách giải:

Gọi \(d\) là khoảng cách từ \(E\;\) đến mặt phẳng \(\left( {SAB} \right)\)

Ta có: \(SD = \sqrt {S{A^2} - A{D^2}} \)\( = \sqrt {{c^2} - \dfrac{{{a^2}{c^2}}}{{{a^2} + {c^2}}}}  = \dfrac{{{c^2}}}{{\sqrt {{a^2} + {c^2}} }}\)

\({V_{S.ADE}} = {V_{E.SAD}}\)\( = \dfrac{1}{3}.\dfrac{1}{2}SD.AD.d\) \( = \dfrac{1}{6}.\dfrac{{{c^2}}}{{\sqrt {{a^2} + {c^2}} }}.\dfrac{{ac}}{{\sqrt {{a^2} + {c^2}} }}.d\) \( = \dfrac{1}{6}.\dfrac{{a{c^3}}}{{{a^2} + {c^2}}}.d\)

Kết hợp với kết quả trong câu a ta suy ra \(d = \dfrac{{b{c^2}}}{{{a^2} + {b^2} + {c^2}}}\).

Chứng minh rằng tổng các khoảng cách từ một điểm bất kì trong một tứ diện đều đến các mặt của nó là một số không đổi.

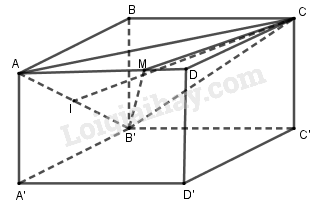
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a,BC = 2a,AA' = a\). Lấy điểm \(M\) trên cạnh \(AD\) sao cho \(AM = 3MD\).

a) Tính thể tích khối chóp \(M.AB'C\)

b) Tính khoảng cách từ \(M\) đến mặt phẳng \(\left( {AB'C} \right)\).

LG câu a

Phương pháp:

- Đổi vị trí đỉnh và đáy của khối chóp, đưa về khối chóp có chiều cao và đáy dễ tính toán.

- Tính thể tích theo công thức \(V = \dfrac{1}{3}Sh\).

Cách giải:

Ta có: \({V_{M.AB'C}} = {V_{B'.ACM}}\).

\({S_{AMC}} = \dfrac{3}{4}{S_{ADC}} = \dfrac{3}{4}.\dfrac{1}{2}.2{a^2} = \dfrac{{3{a^2}}}{4}\)

Do đó \({V_{M.AB'C}} = {V_{B'.ACM}} = \dfrac{1}{3}B'B.{S_{AMC}}\)\( = \dfrac{1}{3}.\dfrac{{3{a^2}}}{4}.a = \dfrac{{{a^3}}}{4}\)

LG câu b

Phương pháp:

- Tính diện tích tam giác \(AB'C\).

- Dựa vào thể tích và diện tích của khối chóp \(M.AB'C\) suy ra khoảng cách theo công thức \(h = \dfrac{{3V}}{S}\).

Cách giải:

Gọi \(h\) là khoảng cách từ \(M\) đến mặt phẳng \(\left( {AB'C} \right)\)

Khi đó \({V_{M.AB'C}} = \dfrac{1}{3}{S_{AB'C}}.h = \dfrac{{{a^3}}}{4}\)

Vì \(A{C^2} = {\rm{ }}B'{C^2} = 5{a^2}\) nên tam giác \(ACB'\) cân tại \(C\). Do đó, đường trung tuyến \(CI\) của tam giác \(ACB'\) cũng là đường cao.

Ta có: \(C{I^2} = {\rm{ }}C{A^2}-{\rm{ }}A{I^2}\)\( = {\rm{ }}5{a^2} - {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2}\) \( = 5{a^2} - \dfrac{{{a^2}}}{2} = \dfrac{{9{a^2}}}{2}\)

Do đó \(CI = \dfrac{{3a}}{{\sqrt 2 }}\)\( \Rightarrow {S_{AB'C}} = \dfrac{1}{2}.\dfrac{{3a}}{{\sqrt 2 }}.a\sqrt 2  = \dfrac{{3{a^2}}}{2}\)

\( \Rightarrow h = \dfrac{{3V}}{S} = \dfrac{{3{a^3}}}{4}:\dfrac{{3{a^2}}}{2} = \dfrac{a}{2}\).

Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a,BC = b,AA' = c\). Gọi \(M\) và \(N\) theo thứ tự là trung điểm của \(A'B'\) và \(B'C'\). Tính tỉ số giữa thể tích khối chóp \(D'.DMN\) và thể tích khối hộp chữ nhật \(ABCD.A'B'C'D'\).

Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a,BC = b,AA' = c\). Gọi \(E\) và \(F\) lần lượt là những điểm thuộc cạnh \(BB'\) và \(DD'\) sao cho \(BE = \dfrac{1}{2}EB',DF = \dfrac{1}{2}FD'\). Mặt phẳng \(\left( {AEF} \right)\) chia khối hộp chữ nhật \(ABCD.A'B'C'D'\) thành hai khối đa diện \(\left( H \right)\) và \(\left( {H'} \right)\). Gọi \(\left( {H'} \right)\) là khối đa diện chứa đỉnh \(A'\). Hãy tính thể tích của \(\left( H \right)\) và tỉ số thể tích của \(\left( H \right)\) và \(\left( {H'} \right)\).

Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(E\) và \(F\) lần lượt là trung điểm của \(B'C'\) và \(C'D'\). Mặt phẳng \(\left( {AEF} \right)\) chia hình hộp đó thành hai hình đa diện \(\left( H \right)\) và \(\left( {H'} \right)\), trong đó \(\left( H \right)\) là hình đa diện chứa đỉnh \(A'\). Tính tỉ số giữa thể tích hình đa diện \(\left( H \right)\) và thể tích hình đa diện \(\left( {H'} \right)\).