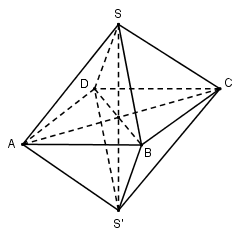
Giả sử \(SABCDS’\) là khối tám mặt đều. Ba đường chéo của nó là \(SS’, AC\) và \(BD\). Bốn điểm \(A, B, C, D\) cách đều hai điểm \(S\) và \(S’\) nên cùng nằm trên một mặt phẳng.Vậy \(ABCD\) là hình thoi, ngoài ra \(S\) cách đều \(A, B, C, D\) nên hình thoi đó là hình vuông. Suy ra hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm của mỗi đường, chúng vuông góc với nhau và có độ dài bằng nhau. Tương tự đối với các cặp đường chéo còn lại.
