1.5
Phương trình dao động điều hoà của một chất điểm là \(x = A\cos \left( {\omega t - {\pi \over 2}} \right)\,cm\). Hỏi gốc thời gian được chọn vào lúc nào ?
A. Lúc chất điểm qua vị trí cân bằng theo chiều dương.
B. Lúc chất điểm qua vị trí cân bằng theo chiều âm.
C. Lúc chất điểm ở vị trí biên x = \(+A\).
D. Lúc chất điểm ở vị trí biên x= \(-A\).
Thay \(t = 0\) vào phương trình \(x = A\cos (\omega t - \dfrac{\pi }{2})\) ta được
\({x_0} = A\cos (\omega .0 - \dfrac{\pi }{2}) = 0\)
Pha dao động tại \(t = 0\) là \(\varphi = - \dfrac{\pi }{2}\) , ta có:
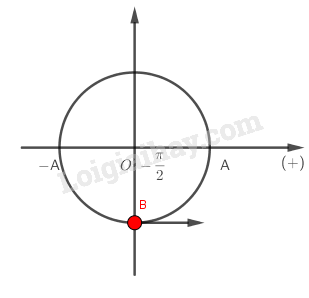
Vậy gốc thời gian là lúc vật qua vị trí cân bằng theo chiều dương.
Chú ý:
Ta có dấu của vận tốc \(v\) và \(\sin (\omega t + \varphi )\) trái nhau, do vậy dựa vào dấu pha dao động ta có thể xác định chiều chuyển động của vật.
Ta có: \(\sin ( - \dfrac{\pi }{2}) = - 1 < 0 \Rightarrow v > 0\)
Chọn A
1.6
Một vật nhỏ dao động điều hoà theo phương trình \(x = 10\cos \left( {\pi t + {\pi \over 6}} \right)\,(cm)\)
Lấy \({\pi ^2} = 10\) Gia tốc của vật có độ lớn cực đại là
A.\(10\pi cm/{s^2}\). B.\(10cm/{s^2}\).
C.\(100cm/{s^2}\). D.\(100\pi cm/{s^2}\).
Từ phương trình \(x = 10\cos \left( {\pi t + {\pi \over 6}} \right)\,(cm)\), ta có \(A = 10(cm)\), \(\omega = \pi (rad/s)\)
Gia tốc có độ lớn cực đại là: \({a_{\max }} = A.{\omega ^2} = 10{\pi ^2} = 10.10 = 100(cm/{s^2})\)
Chọn C
1.7
Một chất điểm dao động điều hoà theo phương trình :\(x = 2\cos \left( {2 \pi t + {\pi \over 2}} \right)\,cm\). Tại \(t = 0,25 s\) chất điểm có li độ bằng
A. \( \sqrt{3} \) cm. B. \( -\sqrt{3} \) cm.
C. \(2 cm\). D. \(-2 cm\).
Thay \(t = \dfrac{1}{4}s\) vào phương trình \(x = 2\cos (2\pi t + \dfrac{\pi }{2})\) ta được:
\(x = 2\cos (2\pi .\dfrac{1}{4} + \dfrac{\pi }{2}) = - 2(cm)\)
Chọn D
Phương pháp giải Thay \(t = 0\) vào phương trình giao động điều hòa, dùng vòng tròn lượng giác xét chiều chuyển động của vật
Vận dụng công thức tính độ lớn gia tốc cực đại: \({a_{\max }} = A.{\omega ^2}\)
Thay thời điểm t vào phương trình dao động điều hòa.