Vì \(\left| {f(x)} \right| = \left\{ \begin{array}{l}f(x),f(x) \ge 0\\ - f(x),f(x) < 0\end{array} \right.\)
Nên để vẽ đồ thị của hàm số \(y = |f(x)|\) ta vẽ đồ thị của hàm số \(y =f(x)\), sau đó giữ nguyên phần đồ thị ở phía trên trục hoành và lấy đối xứng phần đồ thị nằm phía dưới trục hoành qua trục hoành.
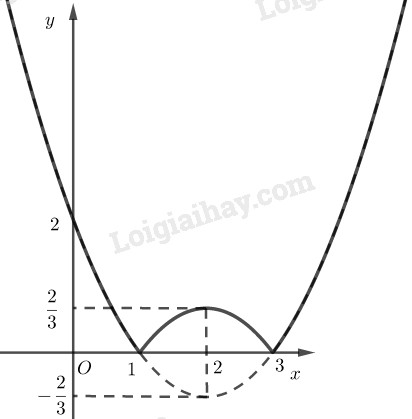
Trong trường hợp này, ta vẽ đồ thị của hàm số \(y = \dfrac{2}{3}{x^2} - \dfrac{8}{3}x + 2\), sau đó giữ nguyên phần đồ thị ứng với các nửa khoảng \(( - \infty ;1]\) và \({\rm{[}}3; + \infty )\).
Lấy đối xứng phần đồ thị ứng với khoảng \((1;3)\) qua trục hoành.
Đồ thị của hàm số \(y = \left| {\dfrac{2}{3}{x^2} - \dfrac{8}{3}x + 2} \right|\) được vẽ trên hình sau (đường nét liền)