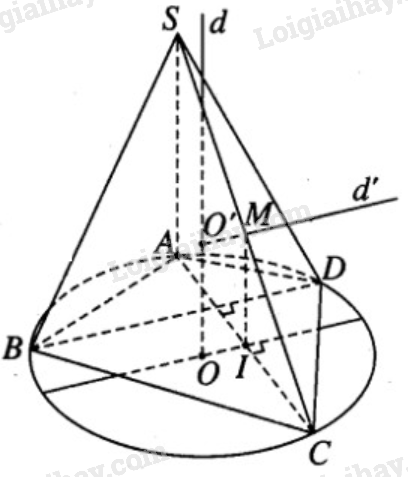
a) Trong mặt phẳng chứa đường tròn tâm O ngoại tiếp tứ giác ABCD ta kẻ đường kính qua O vuông góc với dây cung AC tại I.
Ta có IA = IC và OI // BD. Gọi O’ là tâm mặt cầu đi qua 5 đỉnh của hình chóp.
Khi đó điểm O’ phải nằm trên trục d của đường tròn ngoại tiếp tứ giác ABCD.
Ta có \(\displaystyle d \bot (ABCD)\) tại O. Gọi M là trung điểm của cạnh SC.
Ta có MI // SA nên \(\displaystyle MI \bot (ABCD)\) tại I. Từ M kẻ đường thẳng d’//OI cắt d tại O’.
Vì \(\displaystyle d' \bot (SAC)\) tại M nên ta có O’C = O’S và O’C là bán kính r của mặt cầu ngoại tiếp hình chóp S.ABCD
Ta có \(\displaystyle r = O'C = \sqrt {OO{'^2} + O{C^2}} = \sqrt {M{I^2} + r{'^2}}\)
\(\displaystyle = \sqrt {{{({h \over 2})}^2} + r{'^2}} \) \(\displaystyle = {{\sqrt {{h^2} + 4r{'^2}} } \over 2}\)
b) Vì SA không đổi nên ta có VSABCD lớn nhất khi và chỉ khi SABCD lớn nhất.
Ta có \(\displaystyle {S_{ABCD}} = {1 \over 2}AC.BD\) trong đó AC và BD là hai dây cung vuông góc với nhau.
Vậy AC.BD lớn nhất khi và chỉ khi AC = BD = 2r’ , nghĩa là tứ giác ABCD là một hình vuông.