Cách thứ nhất
Dễ thấy tam giác ABC vuông tại A nên \(\overrightarrow {AC} .\overrightarrow {AB} = 0\) và tam giác SAB đều nên \(\left( {\overrightarrow {SA} ,\overrightarrow {AB} } \right) = {120^0}\).
\(\eqalign{
& \overrightarrow {SC} .\overrightarrow {AB} = \left( {\overrightarrow {SA} + \overrightarrow {AC} } \right).\overrightarrow {AB} \cr
& = \overrightarrow {SA} .\overrightarrow {AB} + \overrightarrow {AC} .\overrightarrow {AB} \cr
& \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {AB} } \right|.\cos 120^\circ = - {{{a^2}} \over 2} \cr
& \Rightarrow \cos \left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = {{\overrightarrow {SC} .\overrightarrow {AB} } \over {\left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {AB} } \right|}} \cr
& = {{ - {{{a^2}} \over 2}} \over {{a^2}}} = - {1 \over 2} \cr}\)
Do đó góc giữa hai đường thẳng \(SC\) và \( AB\) bằng 60°.
Cách thứ hai
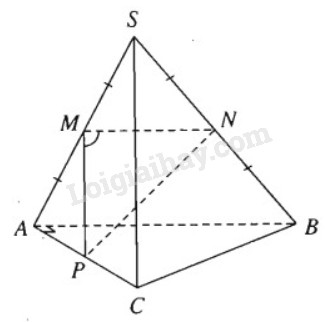
Gọi \(M, N, P\) lần lượt là trung điểm của \(SA, SB, AC\). Để tính góc giữa hai đường thẳng \(SC\) và \(AB\), ta cần tính \(\widehat {NMP}\).
Ta có
\(NB = MP = {a \over 2},S{P^2} = {{3{a^2}} \over 4},B{P^2} = {{5{a^2}} \over 4}\)
\(P{B^2} + S{P^2} = 2N{P^2} + {{S{B^2}} \over 2} \Rightarrow N{P^2} = {{3{{\rm{a}}^2}} \over 4}\)
Mặt khác:
\(N{P^2} = N{M^2} + M{P^2} - 2MN.MP\cos \widehat {NMP}\)
\( \Rightarrow \cos \widehat {NMP} = - {{{{{a^2}} \over 4}} \over {2.{a \over 2}.{a \over 2}}} = - {1 \over 2} \Rightarrow \widehat {NMP} = {120^0}\)
Vậy góc giữa hai đường thẳng \(SC\) và \(AB\) bằng 60°.