\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi\\={4^2} + {2^2} + 2.4.2.\cos (\pi - \dfrac{\pi }{3}) = 12\\ \Rightarrow A = 2\sqrt 3 cm\end{array}\)
Ta có giản đồ Fre-nen:
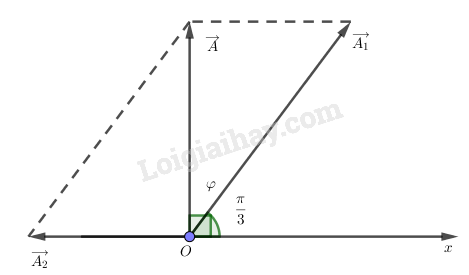
\(\tan \widehat {AO{A_1}} = \dfrac{{{A_2}}}{A} = \dfrac{2}{{2\sqrt 3 }}\)\( \Rightarrow \widehat {AO{A_1}} = \dfrac{\pi }{6}rad\)
\( \Rightarrow \varphi = \widehat {AO{A_1}} + \widehat {{A_1}Ox}\)
\( = \dfrac{\pi }{6} + \dfrac{\pi }{3} = \dfrac{\pi }{2}rad\)
Vậy phương trình dao động tổng hợp là: \(x = 2\sqrt 3 c{\rm{os(10}}\pi {\rm{t + }}\dfrac{\pi }{2})(cm)\)