Gợi ý làm bài
Ta có (h.64)
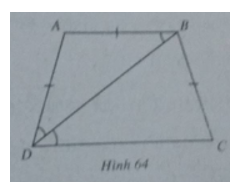
\(\widehat {ABD} = \widehat {ADB}\)
\(\widehat {ABD} = \widehat {BDC}\)
=> \(\widehat {BDC} = \widehat {ADB}\)
Suy ra \(\widehat {BAD} = \pi - 2\widehat {BDC}\)
Từ đó ta có:
\(\eqalign{
& \tan \widehat {BAD} = - \tan 2\widehat {BDC} = - {{2\tan \widehat {BDC}} \over {1 - {{\tan }^2}\widehat {BDC}}} \cr
& = - {{2.{3 \over 4}} \over {1 - {9 \over {16}}}} = - {3 \over 2}.{{16} \over 7} = - {{24} \over 7} \cr} \)
Vì \({\pi \over 2} < \widehat {BAD} < \pi \) nên \(\cos \widehat {BAD} < 0\). Do đó
\(\eqalign{
& \cos \widehat {BAD} = - {1 \over {\sqrt {1 + {{\tan }^2}\widehat {BAD}} }} \cr
& = - {1 \over {\sqrt {1 + {{576} \over {49}}} }} = - {7 \over {25}} \cr} \)
\(\eqalign{
& \sin \widehat {BAD} = \cos \widehat {BAD}.\tan \widehat {BAD} \cr
& = {{ - 7} \over {25}}.{{ - 24} \over 7} = {{24} \over {25}} \cr} \)