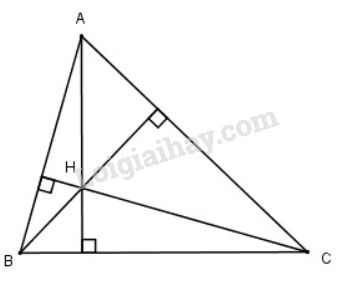
Tọa độ đỉnh \(A\) là nghiệm của hệ:
\(\left\{ \matrix{ 4x + y - 12 = 0 \hfill \cr 2x + 2y - 9 = 0 \hfill \cr} \right. \Rightarrow A({5 \over 2},2)\)
Đường thẳng \(BH : 5x – 4y – 15 = 0\) có vecto chỉ phương \(\overrightarrow u = (4,5)\)
Cạnh \(AC\) vuông góc với \(BH\) nên nhận vecto u làm một vecto pháp tuyến, \(AC\) đi qua \(A({5 \over 2},2)\) và có vecto pháp tuyến \(\overrightarrow u = (4,5)\) nên có phương trình là:
\(4.(x - {5 \over 2}) + 5(y - 2) = 0 \)\(\Leftrightarrow 4x + 5y - 20 = 0\)
Tương tự, tọa độ đỉnh \(B\) là nghiệm của hệ:
\(\left\{ \matrix{ 4x + y - 12 = 0 \hfill \cr 6x - 4y - 15 = 0 \hfill \cr} \right. \Rightarrow B(3,0)\)
\(AH: 2x + 2y – 9 = 0\) có vecto chỉ phương \(\overrightarrow v = ( - 2,2) = 2( - 1,1)\)
\(BC\) vuông góc với \(AH\) nên nhận vecto \(\overrightarrow {v'} = ( - 1,1)\) làm vecto pháp tuyến, phương trình \(BC\) là:
\( - 1(x - 3) + (y - 0) = 0 \)\(\Leftrightarrow x - y - 3 = 0\)
Tọa độ \(H\) là nghiệm của hệ phương trình:
\(\left\{ \matrix{ 5x - 4y - 15 = 0 \hfill \cr 2x + 2y - 9 = 0 \hfill \cr} \right. \Leftrightarrow H({{11} \over 3},{5 \over 6})\)
Đường cao \(CH\) đi qua \(H\) và vuông góc với \(AB\)
Hoàn toàn tương tự, ta viết được phương trình của \(CH\):
\(CH: 3x – 12y – 1= 0.\)