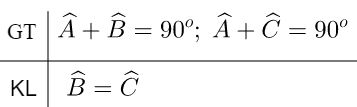
Chứng minh:
\(\widehat B\) phụ với \(\widehat A\) \( \Rightarrow \widehat A + \widehat B = {90^o}\) \( \Rightarrow \widehat B = {90^o} - \widehat A\) (1)
\(\widehat C\) phụ với \(\widehat A\) \(\Rightarrow \widehat A + \widehat C = {90^o}\) \( \Rightarrow \widehat C = {90^o} - \widehat A\) (2)
Từ (1) và (2) suy ra \(\widehat B = \widehat C\).
Bài 7.2
Ghi giả thiết, kết luận và chứng minh định lí: “Hai góc cùng bù với một góc thứ ba thì bằng nhau”.
Phương pháp:
Hai góc bù nhau có tổng số đo bằng \(180^o\).
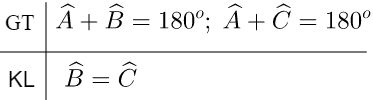
Chứng minh:
\(\widehat B\) bù với \(\widehat A\) \( \Rightarrow \widehat A + \widehat B = {180^o}\) \( \Rightarrow \widehat B = {180^o} - \widehat A\) (1)
\(\widehat C\) bù với \(\widehat A\) \(\Rightarrow \widehat A + \widehat C = {180^o}\) \( \Rightarrow \widehat C = {180^o} - \widehat A\) (2)
Từ (1) và (2) suy ra \(\widehat B = \widehat C\).
Bài 7.3
Ghi giả thiết, kết luận và chứng minh định lí: “Nếu hai đường thẳng \(a, b\) cắt đường thẳng \(c\) và trong các góc tạo thành có một cặp trong cùng phía bù nhau thì \(a\) và \(b\) song song với nhau”.
Phương pháp:
Nếu đường thẳng \(c\) cắt hai đường thẳng \(a, b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc cặp góc đồng vị bằng nhau) thì \(a\) và \(b\) song song với nhau.

Chứng minh:
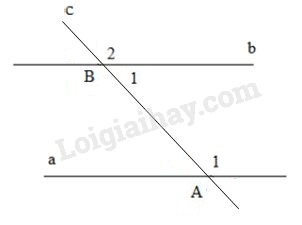
\(\widehat {{A_1}}\) bù với \(\widehat {{B_1}}\) (gt) \( \Rightarrow \widehat {{A_1}} + \widehat {{B_1}} = {180^o} \) \(\Rightarrow \widehat {{A_1}} = {180^o} - \widehat {{B_1}}\) (1)
\(\widehat {{B_1}}\) và \(\widehat {{B_2}}\) là hai góc kề bù nên \(\widehat {{B_1}} + \widehat {{B_2}} = {180^o}\) \(\Rightarrow \widehat {{B_2}} = {180^o} - \widehat {{B_1}}\) (2)
Từ (1) và (2) suy ra \(\widehat {{A_1}} = \widehat {{B_2}}\).
Mà hai góc \(\widehat {{A_1}} \) và \( \widehat {{B_2}}\) ở vị trí đồng vị nên \( a // b.\)