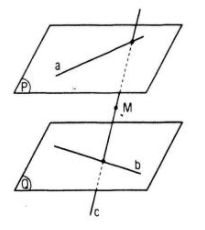
Giả sử c = mp ( M, a) ∩ mp(M, b). Ta cần chứng minh c cắt cả a và b.
Vì c và a cũng nằm trên một mặt phẳng và không thể trùng nhau ( do c qua M và a không đi qua M) nên hoặc c // a hoặc c cắt a. Cũng vậy, hoặc c // b hoặc c cắt b.
Không thể xảy ra đồng thời c // a; c // b vì a và b chéo nhau. Vậy nếu c song song với a và c phải cắt b, tức là c qua một điểm của mp (Q) và song song với a, suy ra c phải thuộc mp (Q), và do đó M thuộc (Q) (trái giả thiết).
Tương tự, không thể có c song song với b.
Tóm lại c cắt a và b.
Nếu còn có đường thẳng c’ khác c đi qua M, cắt cả a và b thì a và b đồng phẳng. Vô lí.
