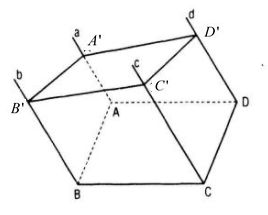
Ta có: \(\left\{ {\matrix{ {a//b} \cr {AD//BC } \cr {a \cap AD=A } \cr } } \right.\Rightarrow \left( {a,d} \right)//\left( {b,c} \right) \)
Tương tự (a, b) // (c, d).
Vì hai mặt phẳng (a, b) và (c, d) song song nhau nên mp(A’B’C’) cắt hai mặt phẳng này
lần lượt theo hai giao tuyến A’B’ và C’D’ song song nhau.
Tương tự A’D’// B’C’.
Vậy A’B’C’D’ là hình bình hành.