Câu 1: Cho hai dãy số thỏa mãn với mọi và thì:
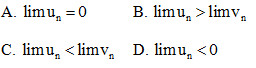
Câu 2: Trong các giới hạn sau, giới hạn nào bằng -1?
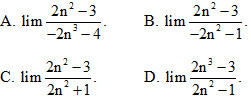
Câu 3: Chọn kết quả đúng: \(\lim \dfrac{{\dfrac{{ - 1}}{3}\sqrt n + 2n}}{{3n}}\) bằng
A. \(\dfrac{{ - 1}}{9}\) B. \(\dfrac{2}{3}\)
C. \( - \infty \) D. Kết quả khác
Câu 4: Cấp số nhân lùi vô hạn\(({u_n})\) có \({u_1} = - 1;q = x;\left| x \right| < 1\). Tìm tổng S và ba số hạng đầu của cấp số này
A. \(S = \dfrac{{ - 1}}{{1 + x}}\)và \( - 1;x; - {x^2}\)
B. \(S = \dfrac{{ - 1}}{{1 + x}}\)và \(1;x;{x^2}\)
C. \(S = \dfrac{{ - 1}}{{1 - x}}\)và \( - 1; - x; - {x^2}\)
D. \(S = \dfrac{{ - 1}}{{1 - x}}\)và \( - 1;x; - {x^2}\)
Câu 5: Tính \(\lim (\sqrt n - \sqrt {n + 1} )\)
A.Không có giới hạn khi \(n \to + \infty \)
B. 0
C. -1
D. Kết quả khác
Câu 6: Chọn kết quả đúng:
A. \(\lim \sqrt {\dfrac{{2n - 7}}{n}} = + \infty \)
B. \(\lim \sqrt {\dfrac{2}{n}} = \sqrt 2 \)
C. \(\lim \sqrt {\dfrac{{2{n^2}}}{{n + 1}}} = \sqrt 2 \)
D. \(\lim \sqrt {\dfrac{{n - 7}}{{2n}}} = \dfrac{{\sqrt 2 }}{2}\)
Câu 7: Tìm \(\lim \sqrt {\dfrac{{7 - 2n}}{{4n + 5}}} \)
A. \(\sqrt {\dfrac{1}{2}} \)
B. \( - \infty \)
C. 0
D. Không có giới hạn khi \(n \to + \infty \)
Câu 8: Giá trị của \(\lim \dfrac{{\sqrt {{n^2} + 1} - \sqrt[3]{{3{n^3} + 2}}}}{{\sqrt[4]{{2{n^4} + n + 2}} - n}}\) bằng
A. \( + \infty \)
B. \( - \infty \)
C. \(\dfrac{{1 - \sqrt[3]{3}}}{{\sqrt[4]{2} - 1}}\)
D. 1
Câu 9: Giới hạn bằng?
A. 0 B. \(\frac{{ - 1}}{2}\)
C. \(\frac{{ - 1}}{{\sqrt 2 }}\) D. \(\frac{1}{{\sqrt 2 }}\)
Câu 10: Kết quả nào sau đây là đúng?
A. Cấp số nhân lùi vô hạn \(({u_n})\)có công bội q thì tổng \(S = \dfrac{u}{{1 - q}}\)
B. Cấp số nhân lùi vô hạn \(({u_n})\)có \({u_1} = 4;q = \dfrac{4}{3}\) thì tổng \(S = - 12\)
C. Cấp số nhân lùi vô hạn \(({u_n})\)có \({u_1} = 15;S = 60\) thì \(q = \dfrac{3}{4}\)
D. Cấp số nhân lùi vô hạn \(({u_n})\)có \({u_1} = - 4;q = - \dfrac{5}{4}\) thì tổng \(S = - 169\)