Đề số 4 - Đề thi vào lớp 10 môn Toán

Câu 1.  Tính giá trị biểu thức \(T = \sqrt {16}  + 5\)

Câu 2. Giải phương trình \(2x - 3 = 1\)

Câu 3.  Tìm giá trị của m để đường thẳng \(\left( d \right):y = 3x + m - 2\) đi qua điểm \(A\left( {0;1} \right)\).

Câu 4. Vẽ đồ thị hàm số \(y =  - 2{x^2}\)

Câu 5. Giải hệ phương trình \(\left\{ \begin{array}{l}3x - 2y = 4\\x + 3y = 5\end{array} \right..\)

Câu 6. Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\;\left( {H \in BC} \right).\)Biết \(AB = 3a,\;\;AH = \dfrac{{12}}{5}a.\) Tính theo \(a\) độ dài \(AC\) và \(BC.\) 

Câu 7. Tìm giá trị của m để phương trình \(2{x^2} - 5x + 2m - 1 = 0\) có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) thỏa mãn: \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{5}{2}.\)

Câu 8. Một đội máy xúc được thuê đào \(20000\;{m^3}\) đất để mở rộng hồ Dầu Tiếng. Ban đầu đội dự định mỗi ngày đào một lượng đất nhất định để hoàn thành công việc, nhưng sau khi đào được \(5000\;{m^3}\) thì đội được tăng cường thêm một số máy xúc nên mỗi ngày đào thêm được \(100\;{m^3},\) do đó đã hoàn thành công việc trong \(35\) ngày. Hỏi ban đầu đội dự định mỗi ngày đào bao nhiêu \({m^3}\) đất?

Câu 9 Cho tam giác ABC có ba góc nhọn \(\left( {AB < AC} \right)\) và có đường cao AH (H thuộc cạnh BC). Gọi D, E lần lượt là trung điểm của AB và AC. Chứng minh DE là tiếp tuyến chung của hai đường tròn lần lượt ngoại tiếp tam giác DBH và ECH.

Câu 10 :Cho đường tròn tâm O bán kính 2R (kí hiệu (O; 2R)) và đường tròn tâm O’ bán kính R (kí hiệu (O’; R)) tiếp xúc ngoài nhau tại A. Lấy điểm B trên đường tròn (O; 2R) sao cho \(\widehat {BAO} = {30^0}\), tia BA cắt đường tròn (O’; R) tại điểm C (C khác điểm A). Tiếp tuyến của đường tròn (O’; R) tại điểm C cắt đường thẳng BO tại điểm E. Tính theo R diện tích tam giác ABE.

Câu 1.

\(T = \sqrt {16}  + 5 = \sqrt {{4^2}}  + 5 = 4 + 5 = 9\)

Câu 2

\(\begin{array}{l}2x - 3 = 1\\2x = 4\\x = 2\end{array}\)

Câu 3.

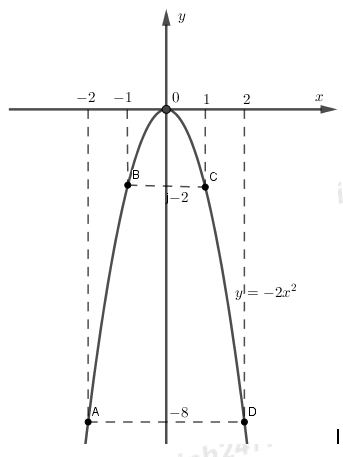
Vẽ đồ thị hàm số \(y =  - 2{x^2}\)

Trên mặt phẳng tọa độ lấy các điểm \(A\left( { - 2; - 8} \right);\,B\,\left( { - 1; - 2} \right);\,\,O\left( {0;0} \right);\)\(\,\,C\left( {1; - 2} \right)\,\,  ;D\left( {2; - 8} \right)\).

Đồ thị của hàm số \(y =  - 2{x^2}\) đi qua các điểm A, B, O, C, D có tọa độ như trên.

Câu 5:

Giải hệ phương trình \(\left\{ \begin{array}{l}3x - 2y = 4\\x + 3y = 5\end{array} \right..\)

\(\left\{ \begin{array}{l}3x - 2y = 4\\x + 3y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - 2y = 4\\3x + 9y = 15\end{array} \right. \)

\(\Leftrightarrow \left\{ \begin{array}{l}x = 5 - 3y\\ - 11y =  - 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 5 - 3.1\end{array} \right. \)

\(\Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right..\)

Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;\;y} \right) = \left( {2;\;1} \right).\)

Câu 6:

Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\;\left( {H \in BC} \right).\)Biết \(AB = 3a,\;\;AH = \dfrac{{12}}{5}a.\) Tính theo \(a\) độ dài \(AC\) và \(BC.\) 

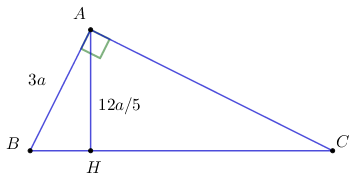
Áp dụng định lý Pi-ta-go cho tam giác \(ABH\) vuông tại \(H\) ta có:

\(B{H^2} = A{B^2} - A{H^2} = 9{a^2} - {\left( {\dfrac{{12}}{5}a} \right)^2} = \dfrac{{81{a^2}}}{{25}} \)

\(\Rightarrow BH = \dfrac{{9a}}{5}.\)

Áp dụng hệ thức lượng cho tam giác \(ABC\) vuông tại \(A\) với đường cao \(AH\;\)ta có:

\(\begin{array}{l}A{H^2} = BH.HC \\\Leftrightarrow HC = \dfrac{{A{H^2}}}{{HB}} = {\left( {\dfrac{{12}}{5}a} \right)^2}:\dfrac{{9a}}{5} = \dfrac{{16a}}{5}.\\ \Rightarrow BC = BH + HC = \dfrac{{9a}}{5} + \dfrac{{16a}}{5} = 5a.\end{array}\)

Áp dụng định lý Pi-ta-go cho tam giác \(ABC\) vuông tại \(A\) ta có:

\(A{C^2} = B{C^2} - A{B^2} = {\left( {5a} \right)^2} - {\left( {3a} \right)^2} = {\left( {4a} \right)^2} \)

\(\Rightarrow AC = 4a.\)

Vậy \(AC = 4a,\;\;BC = 5a.\)

Câu 7:

Tìm giá trị của m để phương trình \(2{x^2} - 5x + 2m - 1 = 0\) có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) thỏa mãn: \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{5}{2}.\)

Phương trình đã cho có hai nghiệm phân biệt \( \Leftrightarrow \Delta  > 0 \Leftrightarrow {5^2} - 4.2.\left( {2m - 1} \right) > 0\)

\(\begin{array}{l} \Leftrightarrow 25 - 16m + 8 > 0\\ \Leftrightarrow 16m < 33\\ \Leftrightarrow m < \dfrac{{33}}{{16}}.\end{array}\)

Với \(m < \dfrac{{33}}{{16}}\) thì phương trình đã cho có hai nghiệm phân biệt \({x_1},\;{x_2}.\)

Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{5}{2}\\{x_1}{x_2} = \dfrac{{2m - 1}}{2}\end{array} \right..\)

Theo đề bài ta có:

\(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{5}{2}\)

\(\begin{array}{l} \Leftrightarrow 2\left( {{x_1} + {x_2}} \right) = 5{x_1}{x_2}\\ \Leftrightarrow 2.\dfrac{5}{2} = 5.\dfrac{{2m - 1}}{2}\\ \Leftrightarrow 10 = 10m - 5\\ \Leftrightarrow 10m = 15\\ \Leftrightarrow m = \dfrac{5}{3}\;\;\left( {tm} \right).\end{array}\) 

Vậy \(m = \dfrac{5}{3}\) thỏa mãn bài toán.

Câu 8:

Máy xúc đào được số \({m^3}\) đất là: \(\dfrac{{20000}}{x}\;\;\left( {{m^3}} \right).\)

Thời gian đội máy xúc đào được \(5000\;{m^3}\) đất là: \(5000:\dfrac{{20000}}{x} = \dfrac{x}{4}\)  (ngày)

Sau khi được tăng thêm số máy xúc thì mỗi ngày đội máy xúc đào được số \({m^3}\) đất là: \(\dfrac{{20000}}{x} + 100\;\;\left( {{m^3}} \right).\)

Số ngày đội máy xúc  đào được \(20000 - 5000 = 15000\;{m^3}\) đất là:

\(15000:\left( {\dfrac{{20000}}{x} + 100} \right) = \dfrac{{150x}}{{200 + x}}\)  (ngày).

Theo đề bài ta có phương trình:

\(\begin{array}{l}\;\;\;\;\dfrac{x}{4} + \dfrac{{150x}}{{200 + x}} = 35\\ \Leftrightarrow x\left( {200 + x} \right) + 4.150x = 35.4\left( {x + 200} \right)\\ \Leftrightarrow {x^2} + 800x = 140x + 28000\\ \Leftrightarrow {x^2} + 660x - 28000 = 0\\ \Leftrightarrow \left( {x - 40} \right)\left( {x + 700} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 40 = 0\\x + 700 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 40\;\;\left( {tm} \right)\\x =  - 7000\;\;\left( {ktm} \right)\end{array} \right..\end{array}\)

Vậy mỗi ngày đội máy xúc đào được  \(\dfrac{{20000}}{{40}} = 500\;{m^3}\) đất.

Câu 9.

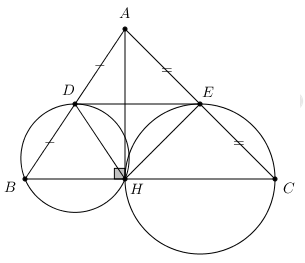
Ta có: D, E lần lượt là trung điểm của AB và AC  nên DE là đường trung bình của tam giác ABC \( \Rightarrow DE//BC\).

\( \Rightarrow \widehat {EDH} = \widehat {DHB}\) (so le trong).

Tam giác AHB vuông tại H, có HD là đường trung tuyến ứng với cạnh huyền AB \( \Rightarrow HD = \dfrac{1}{2}AB = AD = DB\)

\( \Rightarrow \Delta DHB\) cân tại D \( \Rightarrow \widehat {DHB} = \widehat {DBH}\) (hai góc ở đáy của tam giác cân).

\( \Rightarrow \widehat {EDH} = \widehat {DBH}\)

Lại có góc DBH là góc nội tiếp chắn cung DH của đường tròn ngoại tiếp tam giác DBH.

Góc EDH nằm tạo bởi dây cung DH và tia DE với D thuộc đường tròn ngoại tiếp tam giác DBH, nằm ở vị trí góc tạo bởi tia tiếp tuyến và dây cung, chắn cung DH của đường tròn ngoại tiếp tam giác DBH.

\( \Rightarrow DE\) là tiếp tuyến tại D của đường tròn ngoại tiếp tam giác DBH.

Chứng minh tương tự ta có : \(\widehat {DEH} = \widehat {EHC} = \widehat {ECH}\).

Lại có góc ECH là góc nội tiếp chắn cung EH của đường tròn ngoại tiếp tam giác ECH.

Góc DEH nằm tạo bởi dây cung EH và tia ED, nằm ở vị trí góc tạo bởi tia tiếp tuyến và dây cung, chắn cung EH của đường tròn ngoại tiếp tam giác ECH.

\( \Rightarrow DE\) là tiếp tuyến tại E của đường tròn ngoại tiếp tam giác ECH.

Vậy DE là tiếp tuyến chung của hai đường tròn lần lượt ngoại tiếp tam giác DBH và ECH.

Câu 10 :

Cho đường tròn tâm O bán kính 2R (kí hiệu (O; 2R)) và đường tròn tâm O’ bán kính R (kí hiệu (O’; R)) tiếp xúc ngoài nhau tại A. Lấy điểm B trên đường tròn (O; 2R) sao cho \(\widehat {BAO} = {30^0}\), tia BA cắt đường tròn (O’; R) tại điểm C (C khác điểm A). Tiếp tuyến của đường tròn (O’; R) tại điểm C cắt đường thẳng BO tại điểm E. Tính theo R diện tích tam giác ABE.

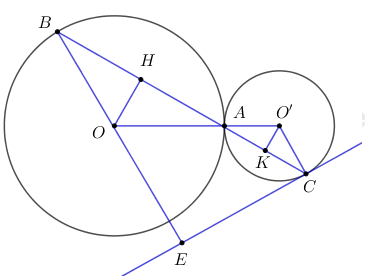
Tam giác OAB có \(OA = OB \Rightarrow \Delta OAB\) cân tại \(O \Rightarrow \widehat {OAB} = \widehat {OBA} = {30^0}\)

Xét tam giác OAB có \(\widehat {AOB} = {180^0} - {30^0} - {30^0} = {120^0}\).

Tam giác O’AC có O’A = O’C \( \Rightarrow \Delta O'AC\) cân tại O’ \( \Rightarrow \widehat {O'CA} = \widehat {O'AC} = \widehat {OAB} = {30^0}\)

\( \Rightarrow \widehat {OBA} = \widehat {O'CA} = {30^0}\), mà hai góc này ở vị trí so le trong \( \Rightarrow OB//O'C\)

\( \Rightarrow \widehat {AO'C} = \widehat {AOB} = {120^0}\)

Ta có \(\widehat {ACE} = \dfrac{1}{2}\widehat {AO'C} = {60^0}\)(góc nội tiếp và góc ở tâm cùng chắn cung AC).

Xét tam giác EBC có \(\widehat {OBA} + \widehat {ACE} = {30^0} + {60^0} = {90^0} \Rightarrow \Delta BCE\) vuông tại E.

Ta có 

\(AC = R\sqrt 3 ;\,\,AB = 2R\sqrt 3 \)

\(\Rightarrow BC = AB + AC = R\sqrt 3  + 2R\sqrt 3  = 3R\sqrt 3 \) 

\( \Rightarrow EC = BC.\cos 60 = 3R\sqrt 3 .\dfrac{1}{2} = \dfrac{{3R\sqrt 3 }}{2}\)

Gọi H, K lần lượt là trung điểm của AB và AC.

\( \Rightarrow OH \bot AB,\;\;O'K \bot AC.\) (mối liên hệ giữa đường kính và dây cung)

Xét \(\Delta AOH\) vuông tại \(H\) có : \(AH = OA.\cos {30^0} = 2R.\dfrac{{\sqrt 3 }}{2} = R\sqrt 3 .\)

\( \Rightarrow AB = 2AH = 2R\sqrt 3 .\)

Xét \(\Delta AO'K\) vuông tại \(K\) có : \(AK = O'A.\cos {30^0} = R.\dfrac{{\sqrt 3 }}{2} = \dfrac{{R\sqrt 3 }}{2}.\)

\(\begin{array}{l} \Rightarrow AC = 2AK = R\sqrt 3 .\\ \Rightarrow BC = AB + AC = 2R\sqrt 3  + R\sqrt 3  = 3R\sqrt 3 .\\ \Rightarrow {S_{BEC}} = \dfrac{1}{2}.BE.EC \\\;\;\;\;\;\;\;\;\;\;\;= \dfrac{1}{2}.3R\sqrt 3 .\dfrac{{3R\sqrt 3 }}{2} = \dfrac{{27R\sqrt 3 }}{4}.\end{array}\)